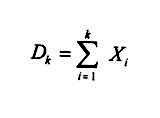ist die Differenz zwischen der Anzahl der "reichen" und der "armen" Wartenden bis zur k-ten Person in der Schlange. Trägt man Dk über i auf, so erhält man einen Polygonzug mit den Ecken ( k; Dk). Gesucht ist die Anzahl N aller Pfade, die im ersten Quadranten verlaufen und D2n = 0 erfüllen., also auf der horizontalen Achse enden. Die Gesamtzahl | Ω | aller denkbaren Pfade ist identisch mit der Anzahl der Möglichkeiten, 2n Elemente linear anzuordnen, von denen jeweils n Elemente identisch sind ( Variationen mit Wiederholungen !). Es gilt somit: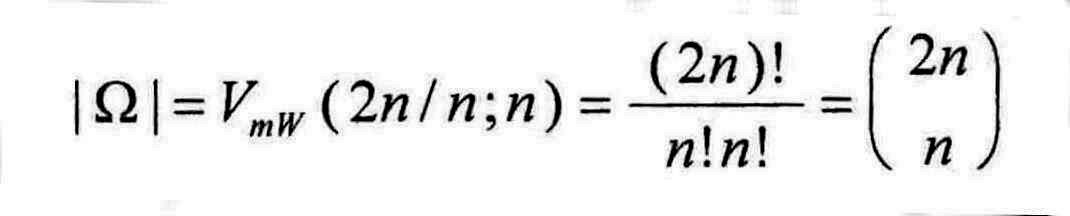
Erlaubte Pfade ( auch zulässige Wege ) im Sinne der Aufgabenstellung sind somit all diejenigen, deren Graph ausschließlich im ersten Quadranten ( D.h.: oberhalb der i-Achse ) verläuft !
Die Anzahl N der erlaubten Pfade lässt sich mit Hilfe der CATALAN-Zahlen ermitteln :
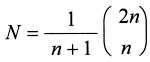( Herleitung: siehe unten ! )Die Wahrscheinlichkeit für einen erlaubten Pfad ist somit:
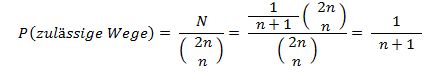
Herleitung der Formel für CATALAN-Zahlen:
 |
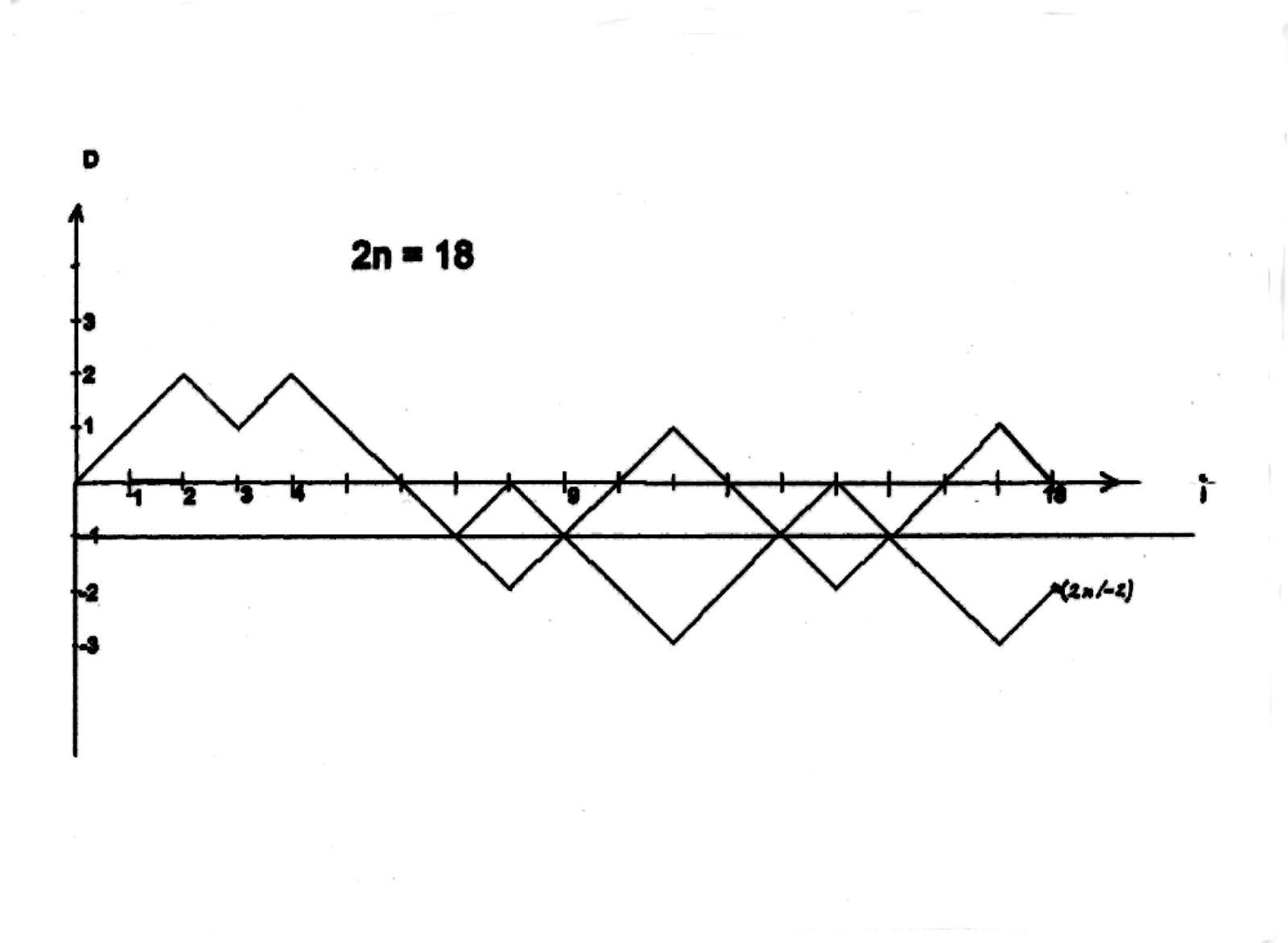Man zeichne einen beliebigen Graphen G. Ist der Graph zulässig im Sinne der Aufgabenstellung, so verläuft er ausschließlich im ersten Quadranten.
Jeder unzulässige Graph U ( Siehe Skizze ! ) muss irgendwann die i-Achse schneiden und die Gerade g: D = -1 berühren. Ab diesem ( ersten ! ) Berührpunkt wird nun G an g gespiegelt. D.h.: Verläuft G nach oben, so muss der gespiegelte Graph nach unten verlaufen ( und umgekehrt ). Alle unzulässigen Graphen enden somit zwangsläufig im Punkt ( 2n / - 2) ! Sie verfügen über n- 1 Intervalle mit positiver Steigung und n + 1 Intervalle mit negativer Steigung !Für die Anzahl der unzulässigen Graphen muss somit gelten : 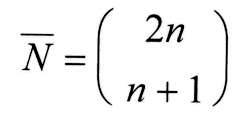 Daraus ergibt sich die Anzahl der zulässigen Wege: 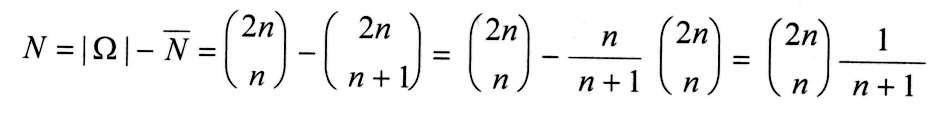 Hinweis: Catalanzahlen tauchen in den verschiedensten kombinatorischen Problemstellungen auf. So beantwortet Catalan z.B. die Frage nach der Anzahl der sinnvollen Klammerungen, wenn man einen Satz von 2n Klammern "()" verwendet. Für n = 3 Klammern-Paare ergibt o.a. Formel 5 Möglichkeiten. ( )( )( ) ; ( )(( )) ; (( ))( ) ; (( )( )) ; ((( ))) |
Anschaulicher - und damit leichter verständlich - als der oben beschrittene Lösungsweg, ist die Verwendung eines Catalan-Gitters zur Lösungsfindung. |
|
|
Jede Person in der Warteschlange, die mit einem 50€-Schein bezahlt, bedeutet in nebenstehendem Gitter einen Schritt nach rechts! Jede Person in der Warteschlange, die mit einem 100€-Schein bezahlt, bedeutet in nebenstehendem Gitter einen Schritt nach oben! Die Zahlen an den Gitter-Kreuzungspunkten beschreiben die Anzahl der zulässigen Zahlungsabfolgen. Im Sinne der Aufgabenstellung muss der erste Ticket-Interessent mit einem 50€-Schein bezahlen. Der Zweite könnte dann bereits mit Wechselgeld bedient werden. .... Immer dann, wenn ein Gitterpunkt oberhalb der roten Winkelhalbierenden rreicht wird, handelt es sich um einen unzulässigen Pfad, da der Theaterbesucher auf sein Wechselgeld warten muss. Für eine überschaubare Anzahl von Besuchern ( in nebenstehender Skizze sind es 20 ) lässt sich die Zahl der zulässigen Pfade durch Abzählen relativ leicht ermitteln. Für einen größeren Besucherandrang empfiehlt sich die Erstellung eines Computer-Programms. Wie gelangt man auf systematischem Weg zu den Zahlen? Für jeden einzelnen in der Schlange gibt es nur zwei Möglichkeiten: Entweder steht vor ihm eine Person mit einem 50€-Schein, oder ein Wechselgeldbedürftiger. Somit ergibt sich für die Anzahl Z der zulässigen Pfade: Z(h,v) = Z(h-1,v) + Z(h,v-1) "h" steht für die Anzahl der Schritte in horizontaler Richtung ( Anzahl der Personen, die mit einem 50€-Schein bezahlen ) "v" steht für die Anzahl der Schritte in vertialer Richtung ( Anzahl der Personen, die mit einem 100€-Schein bezahlen ) Bei der Rekursion ist darauf zu achten, dass die rote Linie nicht überschritten wird! Hinweis: Würde sich zu Beginn des Kartenverkaufs Wechselgeld für n Personen in der Kasse befinden, dann müsste die rote Gerade um n Einheiten längs der vertikalen Achse verschoben werden! |
|
Beispiel: In der Warteschlange befinden sich 8 Prsonen mit einem 50€-Schein und 10 Personen mit einem 100€-Schein. Der Punkt P(8,10) befindet sich oberhalb der roten Linie --> Es gibt keinen erlaubten Pfad im Sinne der Aufgabenstellung! Somit ist P( niemand muss auf Wechselgeld warten ) = 0 ! Beispiel: In der Warteschlange befinden sich 9 Prsonen mit einem 50€-Schein und 7 Personen mit einem 100€-Schein. Die Anzahl der zulässigen Pfade AZ findet man am Gitterpunkt P( 9 , 7 ): AZ = 3432 Die Anzahl der möglichen Pfade ermittelt man über die Formel zur Berechnung von Permutationen mit Wiederholungen: 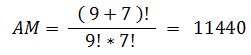 Die gesuchte Wahrscheinlichkeit ergibt sich aus dem Quotientenwer P = AZ / AM = 0,3 |
|
Sollte sich die Programmierung eines Catalan-Rechners als zu aufwändig oder schwierig erweisen, dann kann der Link Catalan-Rechner hilfreich sein!