 |
Einem alten Kinderspiel zufolge, wohnt der Nikolaus in einem Fünfeck. Verbindet man die Ecken in der dargestellten Form, so erhält man ein "Haus", dessen Kanten sich in einem Zug ohne Kantenwiederholung zeichnen lassen. "Wer das nicht kann, kriegt keinen Mann !"
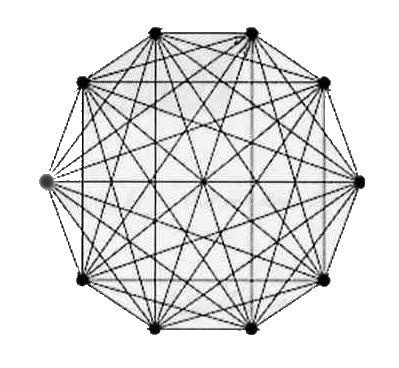
Aus organisatorischen wie repräsentativen Gründen will sich der Nikolaus jetzt vergrößern, zehn Ecken sollten es mindestens sein. Verbindet man jede Ecke ( Zimmer ) mit sämtlichen anderen, so entsteht ein verwirrendes Labyrinth von Gängen. Den Nikolaus beschäftigen nun folgende Fragen:
a: Gibt es auch im neuen Haus eine Möglichkeit, alle Gänge zu begehen, ohne den einen oder anderen mehrmals zu benützen.
b: Wie viele Gänge müssen in jedem Falle mehrfach betreten werden ?
c: Wäre ein Haus mit mehr als 10 Ecken ( Zimmern) denkbar, dessen Gänge die gewünschten Eigenschaft besitzen ?
|
 |