 |
 |
 |
 |
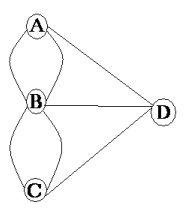
| Im Jahre 1736 befasste sich der Mathematiker Leonhard Euler mit der Frage, ob es einen Rundweg gibt, bei dem man alle 7 Königsberger Brücken über den Pregel genau einmal überquert und wieder zum Ausgangspunkt gelangt. ( Einen solchen Weg bezeichnet man als geschlossene Euler-Tour ! ) |
Es handelt sich um ein topologisches Problem, das Euler mit Methoden löste, die man heute der Graphentheorie zurechnet. O.a. Graph stellt das Brückenproblem schematisch dar. Die Knoten A,B,C und D sind dabei Uferplätze, die verbindenden Kanten stehen für die 7 Brücken. Euler zeigte: Ein Rundweg der gesuchten Art ist genau dann möglich, wenn sich in keinem Knoten ( Uferplätze ) eine ungerade Zahl von Kanten ( Brücken) befindet. Damit war auch gezeigt, dass der Königsberger "Königsweg" ( Alle Brücken auf einem Rundweg genau einmal begehen ) nicht existierte. |
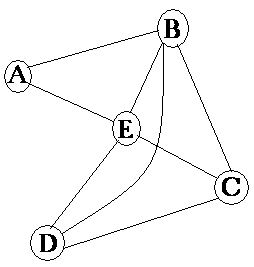
Euler zeigte ferner: Gibt es genau 2 Knoten mit einer ungeraden Anzahl von Kanten, dann existiert immer eine Route, die alle Kanten genau einmal enthält, aber Start- und Zielpunkt können dann nicht mehr identisch sein. Eine solche Route bezeichnet man als offenen Euler-Tour. O.a. Graph erlaubt - ebenso wie "das Haus des Nikolaus" - eine offene Euler-Tour. |
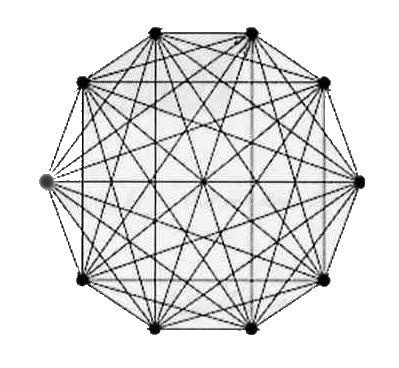
Jeder Knoten des 10-Ecks enthält jeweils 9 Kanten. D.h.: Es gibt 10 Knoten mit ungerader Kantenzahl. Bei einer offenen Euler-Tour sind genau zwei Knoten von ungerader Ordnung. Es verbleiben somit noch 8 Knoten mit ungerader Kantenzahl ( ungerader Ordnung ). Diese acht Knoten werden über 4 Kanten miteinander verbunden. Eine offene Euler-Tour ist also nur dann möglich, wenn man diese vier Kanten ( Gänge ) jeweils 2-mal begeht. Mit den vier zusätzlichen Kanten werden aus den 8 Knoten ungerader Ordnung solche mit einer geraden Kantenzahl. Bei jedem ungeradzahligen Vieleck lässt sich natürlich eine geschlossene Euler-Tour finden ! |
