Die erste Zeile besitzt eine Ziffer.
Die zweite Zeile besitzt 3 Ziffern.
Die dritte Zeile besitzt 5 Ziffern.
....
....
Die i-te Zeile besitzt 2*i - 1 Ziffern.
| Gesucht ist somit: | 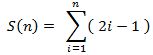 |
Durch Abzählen erhält man unmittelbar:
n = 1 --> S(1) = 1
n = 2 --> S(2) = 4
n = 3 --> S(3) = 9
....
....
Allgemein: S(n) = n2
105! = 1 * 2 * 3 * 4 * .... * 9 * ... * 105.
105! ist somit auch ein Vielfaches von 9. Vielfache von 9 besitzen eine Quersumme Q, die ihrerseits durch 9 ohne Rest teilbar ist!
Die Quersumme der lesbaren Ziffern ergibt Q = 645.
Damit Q durch 9 teilbar wird, ist die Zahl 3 zu addieren.
Bei der unleserlichen Zahl kann es sich somit nur um die Ziffer 3 handeln!
