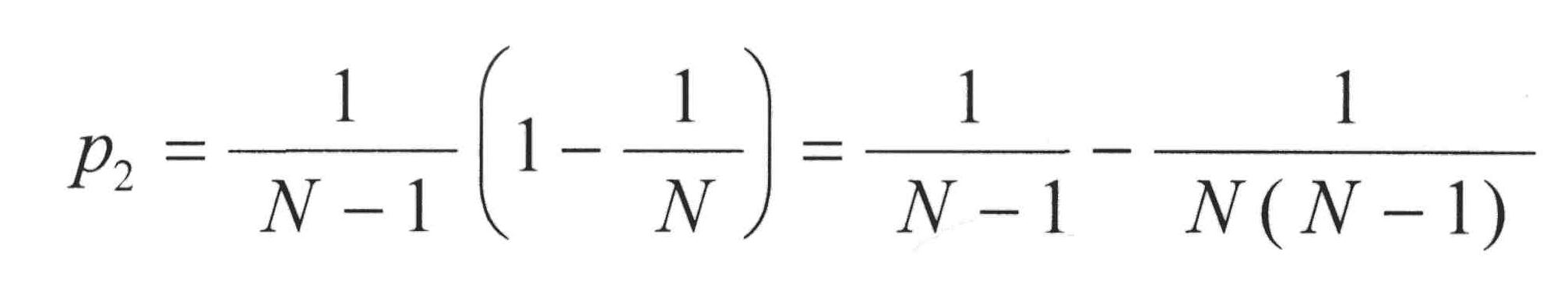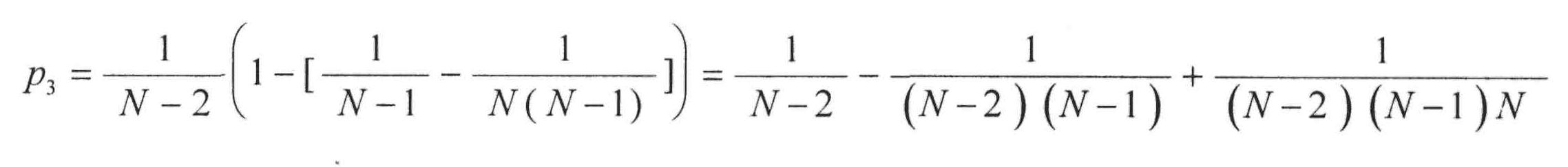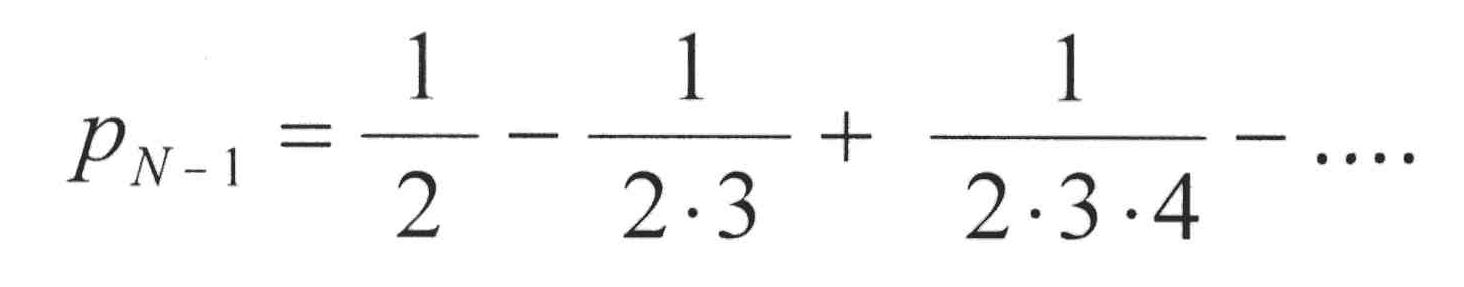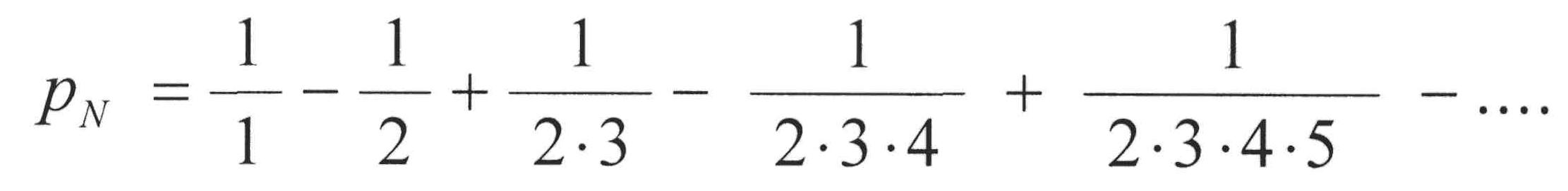Lösungsskizze

Es seien insgesamt N Gäste anwesend, jeder zieht ein Los. Gesucht ist somit die Wahrscheinlichkeit P_x, dass nach N Ziehungen keiner sein eigenes Geschenk erhält. Das ist das Gegenereignis dazu, dass man beim Ziehen bis zum letzten Los gekommen ist und dort erstmals das eigene Geschenk gezogen wird.

Wenn  p_i  die Wahrscheinlichkeit ist, dass mit dem i-ten Los erstmals das eigene Geschenk gezogen wurde, dann gilt:    P_x = 1 - p_N    (*)

Beim i-ten Zug befinden sich noch N - ( i - 1 ) Lose in der Trommel. Die Wahrscheinlichkeit, sein eigenes Geschenk zu ziehen ist somit 1/(N-(i-1)) .
p_i   ist jedoch die Wahrscheinlichkeit, mit dem i-ten Los erstmals das eigene Geschenk zu ziehen! D.h.: Die i - 1 Vorgänger dürfen das eigene Geschenk nicht gelost haben!

Somit ergibt sich für p_i folgende Rekursionsformel:   p_i = ( 1 - p_{i - 1}) / ( N - ( i - 1 ) )   ;   p₁ = 1 / N

Damit ist das Problem prinzipiell gelöst. Man ermittelt der Reihe nach   p₁ , p₂ , p₃ , ... , p_N   und anschließend mit Hilfe von (*) die gesuchte Wahrscheinlichkeit P_x .  Bei N = 300 ist das ein Fall für den Computer.

Lässt sich aus der Rekursionsformel eine explizite Darstellung für p_N finden?
 p₁ = 1 / N


   ....
   ....



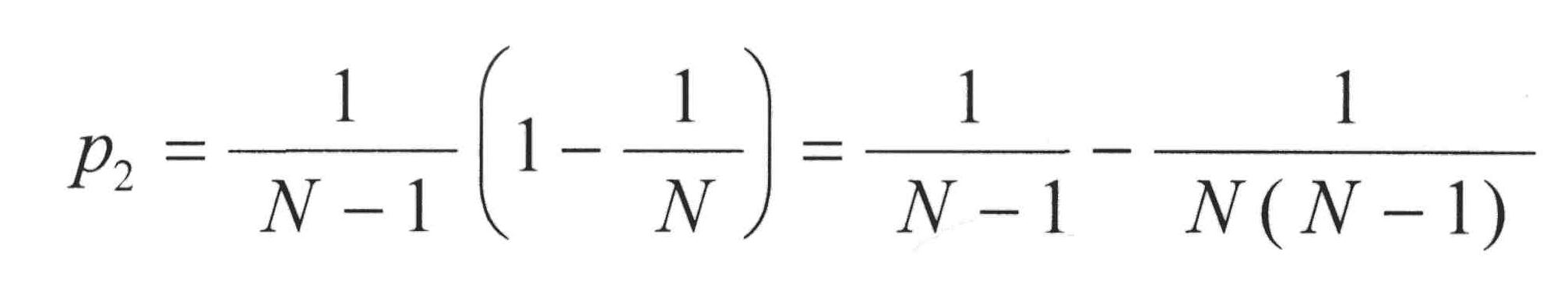
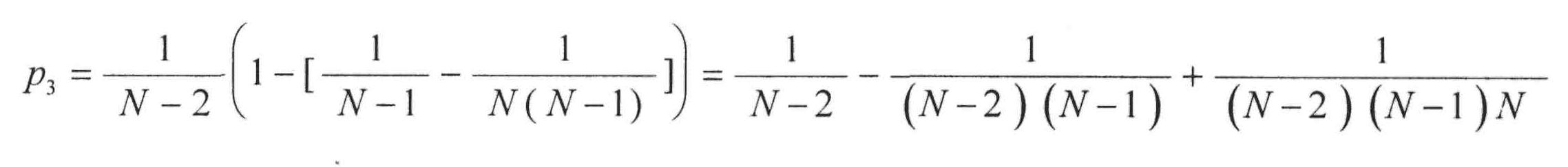
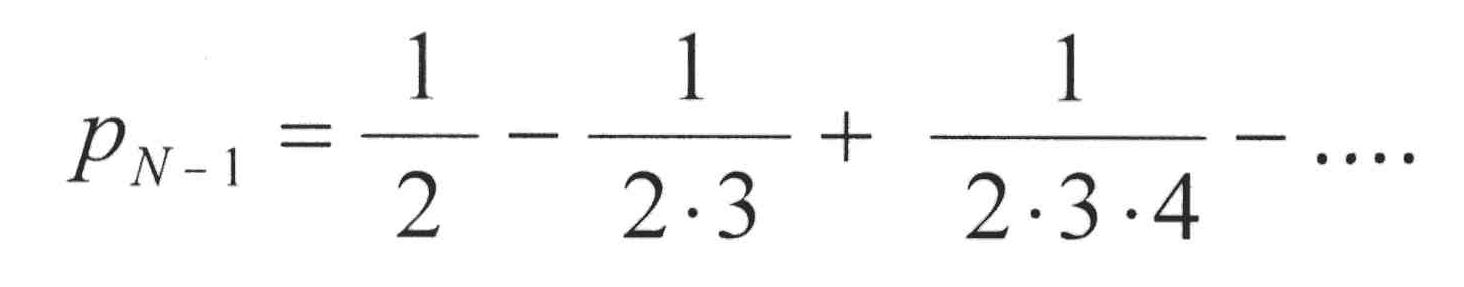
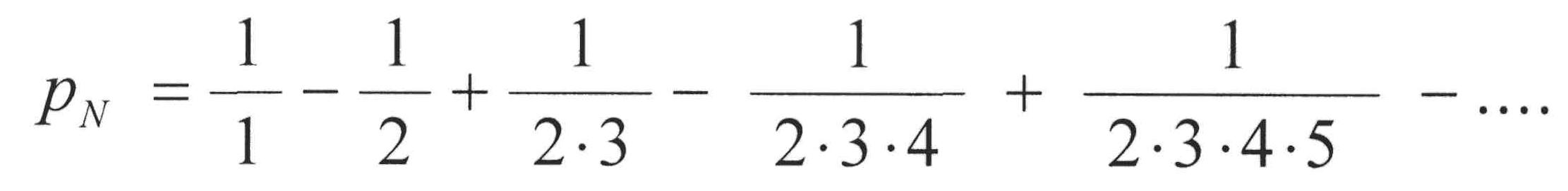
Mit (*) erhält man die gesuchte Wahrscheinlichkeit zu   P_x = 1 - p_N = 1/2!   - 1/3!   + 1/4! - ...

Diese Reihe stellt die Taylor-Entwicklung von 1/e dar!
Die Reihe konvergiert sehr schnell und hat den Grenzwert 1/e.