Lösungsskizze

Hochdruck Wechselnd bewölkt Stark bewölkt Tiefdruck Hochdruck 0,5 0,3 0,15 0,05 Wechselnd bewölkt 0,15 0,65 0,15 0,05 Stark bewölkt 0,1 0,25 0,4 0,25 Tiefdruck 0,08 0,27 0,45 0,2	Nebenstehende Tabelle stellt die Matrix A der Übergangswahrscheinlichkeiten dar. Dem Schema lassen sich z.B. folgende Aussagen entnehmen: -    Ist das Wetter heute wechselnd bewölkt, so kann man morgen mit 65%-iger Wahrscheinlichkeit ebenfalls wechselnde Bewölkung erwarten. -   In nur 8% aller Fälle folgt auf einen verregneten Tag ( Tiefdruck ) ein ausgesprochener Sonnentag. Eine Vorhersage für den übernächsten Tag erhält man durch "Multiplikation" der Matrix A mit sich selbst : A(2) = A x A                         Entsprechend die Prognose für den dritten Tag: A(3) = A x A x A A(4) = A x A x A x A ...... ......
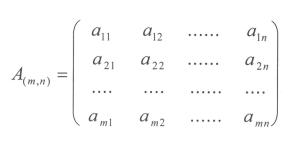
Theorie: Sei   Am,n   eine Matrix mit  m  Zeilen und  n  Spalten. Dann hat die Matrix die Form Das Produkt zweier Matrizen ist nur dann definiert, wenn die Anzahl der Spalten der ersten Matrix gleich der Anzahl der Zeilen der zweiten Matrix ist. D.h., wenn  A   eine   n x m - Matrix ist, so muss   B   eine m x k - Matrix sein! Die Produktmatrix   C ist dann eine   n x k - Matrix. Zur Berechnung des Elements   cij   der Produktmatrix wird die i-te Zeile der ersten Matrix mit der j-ten Spalte der zweiten Matrix "multipliziert" ( im Sinne eines Skalarprodukts ). D.h.: 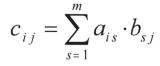   Beispiel:  ;      →
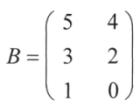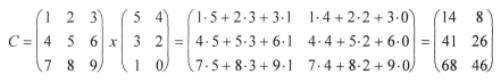
Zurück zur Aufgabenstellung Gegeben ist die Übergangsmatrix 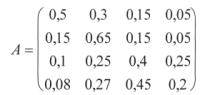      Gesucht ist A3 ( Vorhersage für über-übermorgen! )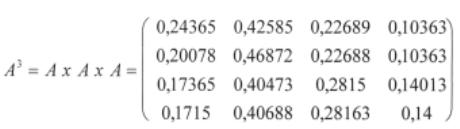    Der Matrix A3 entnimmt Egon: Unter der Voraussetzung, dass das Wetter heute miserabel ist, kann man mit 17,15%-iger Wahrscheinlichkeit davon ausgehen, dass in drei Tagen die Sonne von einem wolkenlosen Himmel lacht. Wie hoch ist, langfristig gesehen, der Anteil der Tage mit Sonnenschein pur ? Der Matrix A entnimmt man folgenden Ansatz: I:       S = 0,5 S + 0,15 Lb + 0,1 Sb + 0,08 T II:      Lb = 0,3 S + 0,65 Lb + 0,25 Sb + 0,27 T III:    Sb = 0,15 S + 0,15 Lb + 0,4 Sb + 0,45 T IV :   T = 0,05 S + 0,05 Lb + 0,25 Sb + 0,2T S:    Sonnenschein pur Lb:   Leicht bewölkt Sb:   Stark bewölkt T:    Tief Dieses Gleichungssystem erweist sich als redundant ! D.h., eine Gleichung kann weggelassen werden ( z.B. Nr. IV ). Damit fehlt eine Gleichung zur eindeitigen Lösung des Systems ! Irgendein Wetter herrscht mit 100%-iger Sicherheit. Also gilt:     S + Lb + Sb + T = 1    Diese Gleichung ergänzt das System und ermöglicht eine eindeutige Lösung. Sonnenschein    ≈  21,7% Lb  ≈  43,82% Sb  ≈  24,14% T    ≈  10,34%