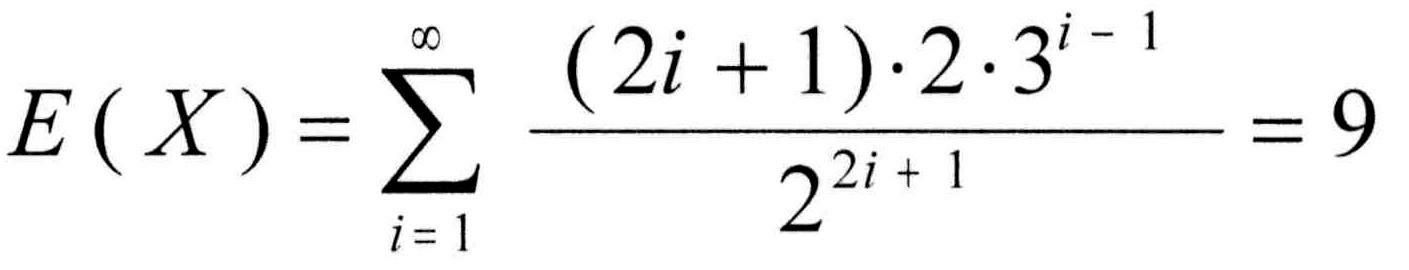l3------l2------l1------ M ------r1------r2------r3
Sam fürchtet die Positionen l3 und r3, sind sie doch gleichbedeutend mit einem kühlen Bad.
Ausgehend von der Brückenmitte M kann er frühestens beim 3. Schritt ins Wasser plumpsen. Geschieht das nicht, so darf er sich beim nächsten Schritt sicher fühlen. Absturzgefahr besteht nur bei einer ungeraden Anzahl von Schritten!
Sei X die Zufallsgröße, die der Anzahl der Schritte die jeweilige Absturzwahrscheinlichkeit zuordnet, dann stellt W = { 3 ; 5 ; 7 ; .... x2i+1 ; .....} die Wertemenge der Zufallsgröße X dar. Der Erwartungswert E(X) - das ist die durchschnittlich zu erwartende Anzahl der Schritte, die zum Absturz führen - ergibt sich zu
E(X) = 3*p(3) + 5*p(5) + 7*p(7) + ... + (2i + 1)*p(x2i + 1) + ..... ; i ε N
D.h.: E(X) = 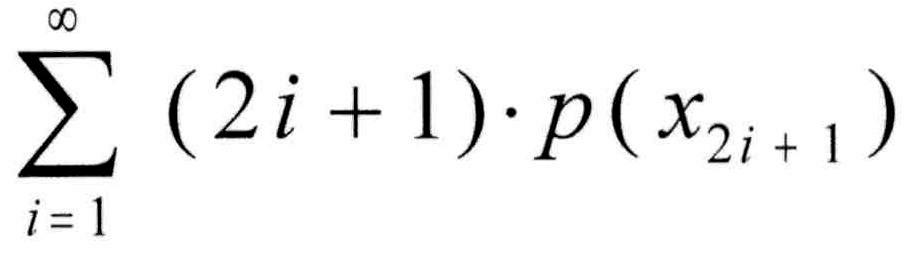 (*)
(*)
Die Wahrscheinlichkeiten p(x2i + 1) lassen sich kombinatorisch, oder mit Hilfe eines Baumdiagramms ermitteln. Es ergibt sich :
p(3) = 2/23 ; p(5) = 6/25 ; p(7) = 18/27 ; p(9) = 54/29 ; ... ; p(2i + 1) = 2*3i-1/22i + 1 ; ...
Der gesuchte Erwartungswert ergibt sich mit Hilfe von (*) zu : 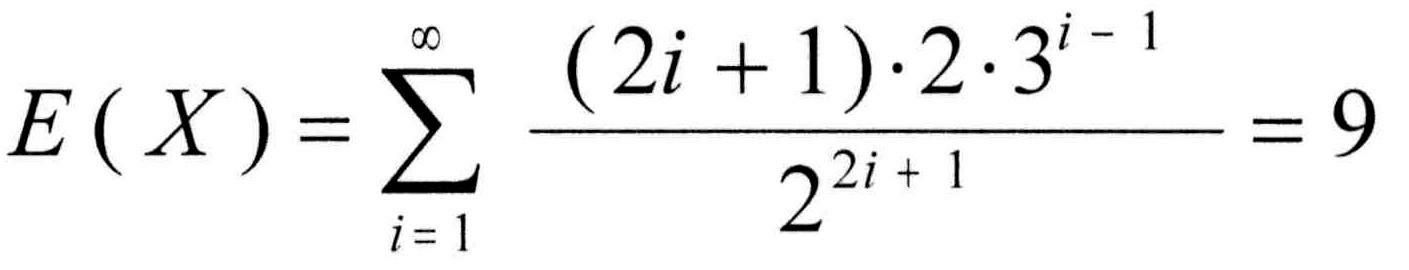
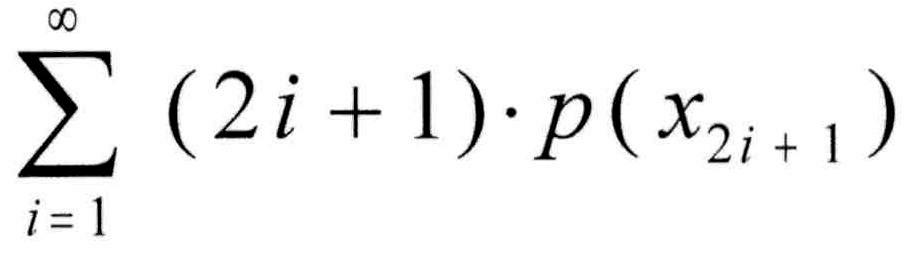 (*)
(*)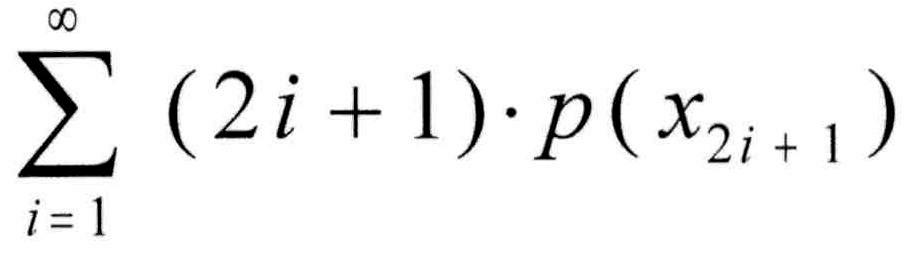 (*)
(*)