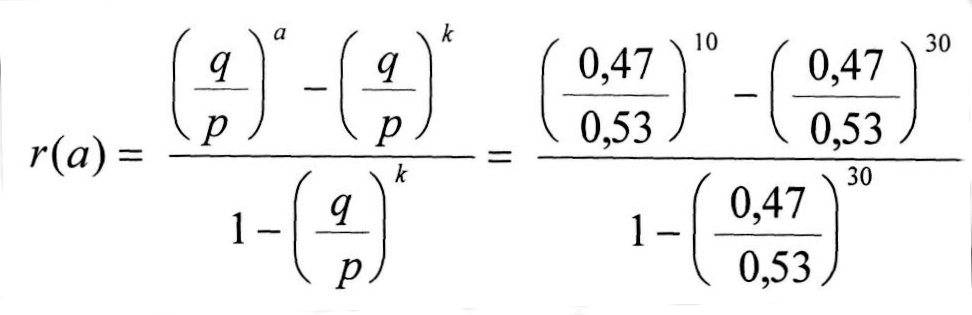
Wenn A ein Spiel mit der Wahrscheinlichkeit p gewinnt, so gewinnt B mit q = 1 - p.
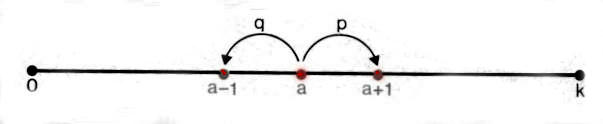
Die Skizze veranschaulicht das Ruinproblem aus der Sicht des Spielers A. Zu Spielbeginn befindet sich A an der Stelle a. Der Spieler bewegt sich nach jedem Spiel einen Schritt nach rechts, falls er gewonnen hat, andernfalls macht er einen Schritt nach links. Die Position von A gibt dann zu jedem Zeitpunkt das verfügbare Kapital an. Die Aufgabe erinnert an "Sam the drunk"! A absolviert auf der Strecke von 0 - k eine Irrfahrt mit Start in a. Gelangt der Spieler dabei nach 0 oder k, so ist das Spiel beendet. Im Punkt 0 ist A ruiniert, in k hat B sein Startkapital restlos verspielt.
r(a) sei die Wahrscheinlichkeit, dass die Irrfahrt im Punkt 0 endet, wenn sich der Spieler im Punkt a befindet.
a) Von a aus gelangt der Spieler mit der Wahrscheinlichkeit p nach a + 1 und von dort mit der Wahrscheinlichkeit r(a + 1) nach 0. Somit ist p * r(a + 1) die Ruinwahrscheinlichkeit für den Fall, dass der erste Schritt nach rechts geht.
b) Von a aus gelangt der Spieler mit der Wahrscheinlichkeit q nach a - 1 und von dort mit der Wahrscheinlichkeit r(a - 1) nach 0. Somit ist q * r(a - 1) die Ruinwahrscheinlichkeit für den Fall, dass der erste Schritt nach links geht.
c) Da sich die Möglichkeiten a) und b) gegenseitig ausschließen und es keine weiteren Alternativen gibt, folgt:
r(a) = p * r(a + 1) + q * r(a - 1) oder p * r(a + 1) + q * r(a - 1) - r(a) = 0
mit den Randbedingungen r(0) = 1 und r(k) = 0
Die Randbedingungen ergeben sich aus der Aufgabenstellung:
Wenn a = 0 ist, dann ist Spieler A mit Sicherheit ruiniert. → r(0) = 1
Wenn a = k ist, dann ist Spieler B ruiniert und A kann nicht mehr ruiniert werden. → r(k) = 0
Gleichung c) stellt eine homogene, lineare Differenzengleichung mit konstanten Koeffizienten dar. Die Theorie der Differenzengleichungen füllt Bücher. Deshalb versuchen wir Lösungen zu "erraten" und deren Richtigkeit durch Einsetzen in Gleichung c) zu verifizieren.
Gesucht ist eine Funktion a → r(a) so, dass die Differenzengleichung c) sowie die Randbedingungen erfüllt sind. Wir versuchen r(a) zu "erraten".
Erster Versuch:
Es wäre schön, wenn r(a) linearen Charakter hätte. Dann ließe sich r(a) in der Form r(a) = m*a + s darstellen. → r(a - 1) = m * (a - 1) + s und r(a + 1) = m * (a + 1) + s
Wir prüfen, ob unser Ansatz Gleichung c) erfüllt. Durch Einsetzen wird c) zu p * [m * (a + 1) + s] + q * [m * (a - 1) + s] - [m * a + s] = 0 →
m*a*(p + q) + m*(p - q) + s*(p + q) = m*a + s; Da p + q = 1 gelten muss → m*a + m*(p - q) + s = m*a + s
Für den Fall, dass p = q ist, entfällt der mittlere Term auf der linken Gleichungsseite und die Differenzengleichung c) ist mit r(a) = m*a + s tatsächlich erfüllt!
Nun gilt es, die Konstanten m und s so zu bestimmen, dass auch die Randbedingungen erfüllt sind.
I: r(0) = m*0 + s = 1 → s = 1
II: r(k) = m*k + s = 0 → m*k + 1 = 0 → m = -1/k
Für den symmetrischen Fall, dass p = q = 1/2 ist, ergibt sich die Ruinwahrscheinlichkeit für A zu r(a) = 1 - a/k
Beispiel: Beide Spieler besitzen die gleiche Gewinnwahrscheinlichkeit p = q = 1/2. A bringt a =10 € mit und b = 20 €. Der Einsatz beträgt jeweils einen Euro pro Spiel.
Dann berechnet sich die Wahrscheinlichkeit, dass sich A ruiniert zu r(a) = 1 - a/k = 1 - a/(a + b) = 1 - 10/30 = 2/3
Unbeantwortet ist immer noch die Frage nach der Ruinwahrscheinlichkeit für den asymmetrischen Fall p ≠ q. Deshalb machen wir einen weiteren Versuch.
Zweiter Versuch:
Wir überprüfen, ob sich r in der Form r(a) = ca darstellen lässt.
r(a) = ca → r(a + 1) = ca + 1 und r(a - 1) = ca - 1
Unser Lösungsansatz erweist sich genau dann als richtig, wenn er die Differenzengleichung c) erfüllt ! Wir prüfen durch Einsetzen in c).
p * r(a + 1) + q * r(a - 1) - r(a) = p * ca + 1 + q * ca - 1 - ca = 0 ? →
ca - 1(p*c2 - c + q) = 0 → Der Ansatz erweist sich somit als richtig, für den Fall, dass der zweite Faktor gleich 0 ist!
p*c2 - c + q = 0 →
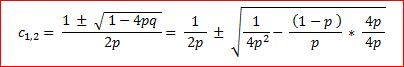 →
→ 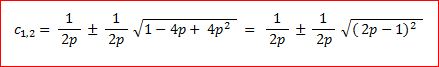 →
→ 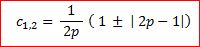 →
→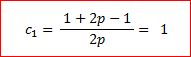 →
→ 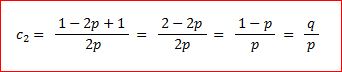
Somit erfüllt der Ansatz r(a) = x1*c1 + x2*( c2 )a = x1*1 + x2*( q / p )a tatsächlich die Differenzengleichung c) !
Nun gilt es, die konstanten Koeffizienten x1 und x2 an die Randbedingungen r(0) = 1 und r(k) = 0 anzupassen.
|
r(0) = 1 → x1 + x2 = 1 r(k) = 0 → x1 + x2( q / p )k = 0 |
Das Gleichungssystem besitzt die Lösungen 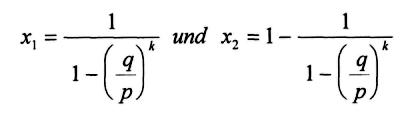
|
Somit ergibt sich: 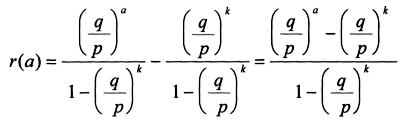
|
|