Lösungsskizze zum Pferderennen
Die Pferde können wie folgt einlaufen:
1: Der Einlauf erfolgt in 6 "Gruppen".
D.h.: Alle Pferde erreichen das Ziel einzeln ( zu unterschiedlichen Zeiten ). In diesem Fall sind 6! = 720 verschiedene Zielankünfte denkbar.
2: Der Einlauf erfolgt in 5 "Gruppen".
D.h.: Zwei Pferde passieren zeitgleich die Ziellinie. In diesem Fall gibt es Kombinationen
ohne Wiederholungen( 2 aus 6 ) = 15 unterschiedliche Paare, die gleichzeitig das Ziel erreichen.
Zu jedem der 15 möglichen Fälle gibt es 5! unterschiedliche Platzierungen. Insgesamt sind somit
15 * 5! = 1800 unterschiedliche Zielankünfte in 5 Gruppen denkbar.
3: Der Einlauf erfolgt in 4 "Gruppen".
D.h.: Drei Pferde passieren zeitgleich die Ziellinie, oder 2 Paare sind jeweils zeitgleich.
Es gibt insgesamt S(6,4) = 65 ( * Siehe Stirling-Formel!! ) Möglichkeiten, aus einer Menge mit 6 Elementen 4 disjunkte,
nichtleere Teilmengen ( "Gruppen" ) zu bilden.
Zu jedem der 65 möglichen Fälle gibt es 4! unterschiedliche Platzierungen. Insgesamt sind somit
65 * 4! = 1560
unterschiedliche Zielankünfte in 4 Gruppen denkbar.
4: Der Einlauf erfolgt in 3 "Gruppen".
Es gibt insgesamt S(6,3) = 90 * Möglichkeiten, aus einer Menge mit 6 Elementen 3 disjunkte, nichtleere Teilmengen ( "Gruppen" ) zu bilden.
Zu jedem der 90 möglichen Fälle gibt es 3! unterschiedliche Platzierungen. Insgesamt sind somit
90 * 3! = 540
unterschiedliche Zielankünfte in 3 Gruppen denkbar.
5: Der Einlauf erfolgt in 2 "Gruppen".
Es gibt insgesamt S(6,2) = 31 * Möglichkeiten, aus einer Menge mit 6 Elementen 2 disjunkte, ;nichtleere Teilmengen ( "Gruppen" ) zu bilden.
Zu jedem der 31 möglichen Fälle gibt es 2! unterschiedliche Platzierungen. Insgesamt sind somit
31 * 2! = 62
unterschiedliche Zielankünfte in 2 Gruppen denkbar.
6: Der Einlauf erfolgt in einer Gruppe.
Es gibt insgesamt S(6,1) = 1 * Möglichkeiten ( Alle Pferde kommen gleichzeitig ins Ziel ).
Die Lösung der Aufgabe ergibt sich somit aus der Addition aller sechs Möglichkeiten.
Bei 6 Pferden sind somit 4683 unterschiedliche Zieleinläufe denkbar !
*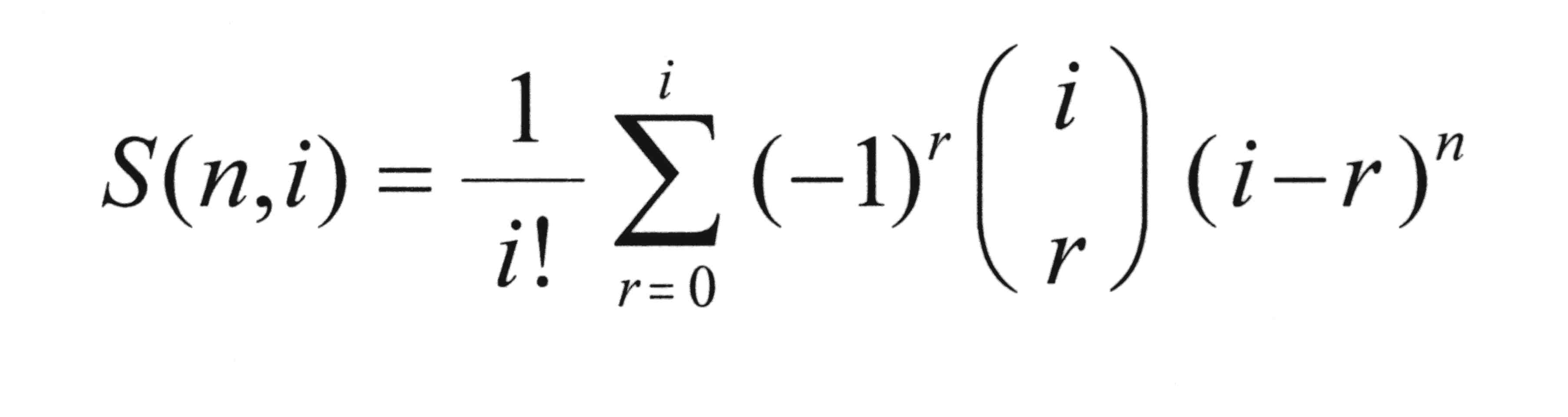 Die Formel zur Berechnung von S(n,i) wurde von dem Iren James STIRLING ( 1692 - 1770 ) gefunden und trägt seinen Namen.
Die Formel zur Berechnung von S(n,i) wurde von dem Iren James STIRLING ( 1692 - 1770 ) gefunden und trägt seinen Namen.
Unter Verwndung der Stirling-Zahlen S(Pferde , Gruppen ) ergibt sich die Anzahl der verschiedenen Zieleinläufe zu



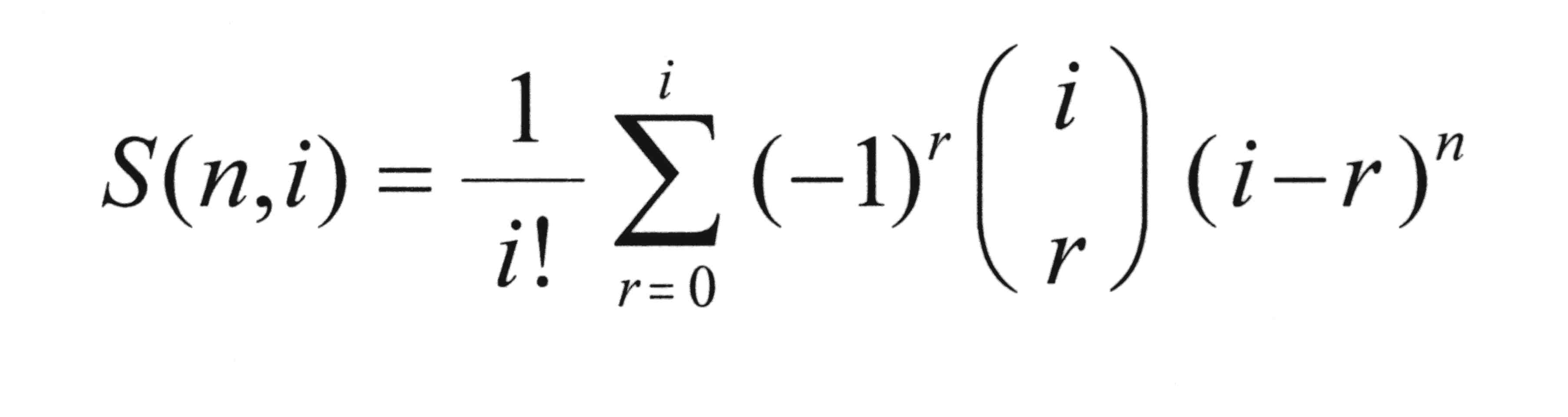 Die Formel zur Berechnung von S(n,i) wurde von dem Iren James STIRLING ( 1692 - 1770 ) gefunden und trägt seinen Namen.
Die Formel zur Berechnung von S(n,i) wurde von dem Iren James STIRLING ( 1692 - 1770 ) gefunden und trägt seinen Namen.

