Optimal im Sinne der kürzesten Wegstrecke wäre sicherlich eine Route, die bei H beginnt, alle Wege genau einmal enthält und schließlich wieder bei H endet. Eine solche Route wird als geschlossene EULER-Tour bezeichnet. Rundtouren dieser Art sind genau dann möglich, wenn jeder Knoten des Graphen eine gerade Anzahl von Kanten besitzt. Das ist bei unserer Parkanlage in den Punkten A, B, F, G, H und I nicht der Fall ! Es gibt somit keinen geschlossenen Rundweg der Streckenwiederholungen vermeidet! 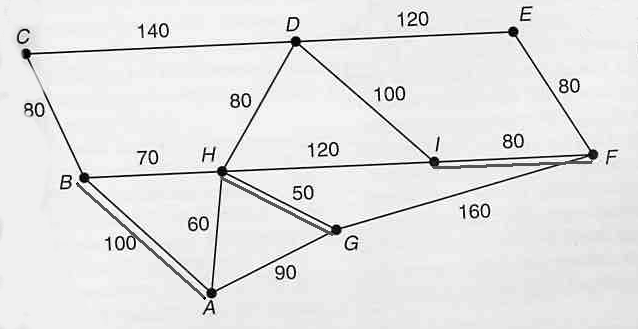Um die Voraussetzungen für einen geschlossenen Rundweg zu schaffen, müssen somit alle Knoten ungerader Ordnung zu solchen mit gerader Ordnung gemacht werden. Dies gelingt durch paarweise Verbindung der Knoten ungerader Ordnung. ( D.h.: Einige Wegstrecken müssen doppelt begangen werden! ) Für die Verbindungen kommen mehrere Möglichkeiten in Betracht. Unter dem Gesichtspunkt der Streckenminimierung wird man die Knoten AB, HG und IF verbinden ( Siehe Skizze! ). Die kürzeste Wegstrecke auf einer EULER-Tour durch den Park ist somit 1330 + 230 = 1560 Meter lang. Ein möglicher Weg durch die Parkanlage wäre z.B.:   HIDEFIFGHABAHBCDH