Eine logische Katastrophe?

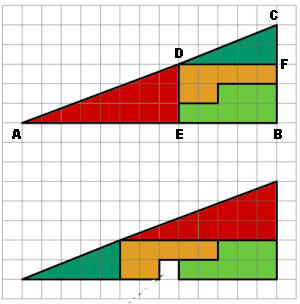
Die gleichfarbigen Elemente der beiden Dreiecke sind tatsächlich kongruent ( D.h., sie besitzen gleiche Winkel , Seitenlängen und Flächen) ! Die Abmessungen der Teilfiguren sind dem unterlegten Raster zu entnehmen:   AE = 8 Längeneinheiten ; ED = 3 ; DF = 5 ; FC = 2. Dem aufmerksamen Betrachter entgeht nicht, dass die Basiswinkel der beiden Dreiecke unterschiedlich sind ! D.h.:   Winkel(EAD)  ≠  Winkel(FDC)   !!    [ Winkel(EAD) = atan(3/8) = atan(0,375) ≈ 20,556°    ; Winkel(FDC) = atan(2/5) = atan(0,4) ≈ 21,8° ] Somit handelt es sich bei nebenstehender Figur nicht um ein Dreieck ( ABC ) , sondern um ein Viereck ( ABCD ). Je geringer die Differenz der Winkel (EAD) und (FDC), desto perfekter die optische Täuschung. Gleichzeitig wird die nach der Umorientierung "fehlende" Fläche mit zunehmender Angleichung der Winkel immer kleiner. Neben annähernd gleichen Dreieckswinkeln sollte die Figur (AEBFCDA) aus didaktischen Gründen folgende Eigenschaften aufweisen: 1:   Winkel(EAD) ≈ Winkel(FDC) 2:   Alle Kathetenlängen sollten der Menge der natürlichen Zahlen entstammen. 3:   Die "fehlende" Fläche sollte möglichst genau einer Flächeneinheit entsprechen !

Zur Erinnerung:

Die Folge der Fibonacci-Zahlen ist rekursiv wie folgt definiert:   an = an-1 + an-2    mit a0 = a1 = 1. F = { 1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34, 55, 89 , 144 , 233 , 377 , 610 , ..... } Mit Hilfe der Binet-Formel lässt sich das n-te Glied der Folge explizit berechnen :    Fibonacci-Zahlen treten in der Natur häufig auf ( Sonnenblumen ; Kiefernzapfen .... ) Durch diese spiralförmige Anordnung der Blätter um die Sprossachse erzielt die Pflanze die beste Lichtausbeute. Der Versatz der Blätter um das irrationale Verhältnis des Goldenen Winkels sorgt dafür, dass nie Perioden auftauchen, wie es z. B. bei 1/4 der Fall wäre (0° 90° 180° 270° | 0° 90° …). Dadurch wird der denkbar ungünstigste Fall vermieden, dass ein Blatt genau senkrecht über dem anderen steht und sich so die jeweils übereinanderstehenden Blätter maximalen Schatten machen oder maximale ‚Lichtlücken‘ entstehen. Wissenschaftshistorisch ist hierfür das Buch  'On Growth and Form'   von D'Arcy Wentworth Thompson (1917) grundlegend.

Einige Eigenschaften der F-Folge

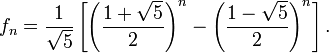
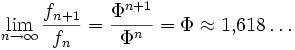
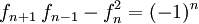
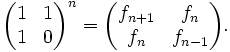a)   Eine Beziehung zwischen den Elementen der Folge :                  fn+1 * fn-2 - fn-1 * fn = (-1)(n-1) b)   Eine Beziehung zwischen den Elementen der Folge :                  c)   Eine weitere Beziehung zwischen den Elementen der Folge :    d)    Wie von Johannes Kepler festgestellt wurde, nähert sich der Quotient zweier aufeinander folgender Fibonacci-Zahlen        dem Goldenen Schnitt Φ an. Der Kehrwert ,    fn / fn+1   nähert sich folglich dem Wert   1 / Φ   = 0,618....    an.

Wie lässt sich Eigenschaft 3 erfüllen ? Die "fehlende Fläche soll nach Änderung des Arrangements der Teilfiguren genau eine Flächeneinheit betragen ! O.a. Skizze gibt die Verhältnisse der Ausgangsfigur in überzeichneter Form wieder. Die Forderung nach Eigenschaft 3 bedeutet, dass das gelbe Dreieck ADC die Fläche  1/2   aufweisen muss.

Sei Winkel(EAD = α    ,    Winkel(FDC) = β    und    Winkel(CDA) = γ Aus   FADC = 1/2    →    AD * DC * sin(γ) / 2 = 1/2    →    AD * DC * sin(γ) = 1    (*) Die Beziehung    γ = 180 + α - β    entnimmt man unschwer nebenstehender Skizze. Somit:    sin(γ) = sin(180 + α - β) = sin(β - α) = cos(α) sin(β) - sin(α) cos(β) sin(γ) eingesetzt in (*)    →     AD * DC * [ cos(α) sin(β) - sin(α) cos(β) ] = 1    →        → AE  *  FC  -   DE * DF  =    1             (**)                 Von den Fibonacci-Zahlen wissen wir: fn+1 *  fn-2  -   fn-1 *  fn    =  (-1)(n-1)   (***)               ( Siehe Eigenschaft a ! ) Dem Vergleich von (**) und (***) entnimmt man, dass Eigenschaft 3 immer dann erfüllt ist, wenn    DF = fn   ,    AE = fn+1   ,    DE = fn-1   und    FC = fn-2       ( mit ungeradem n !! )  gilt. Z.B.:     DF = f5 = 5     ,    AE = f6 = 8     ,   DE = f4 = 3   ,   FC = f3 = 2 Oder:    DF = f7 = 13   ,    AE = f8 = 21   ,   DE = f6 = 8   ,   FC = f5 = 5