Lösung: Der Käfer auf dem Würfel

Sei die "Entfernung" des Käfers vom Ziel die Anzahl der Kanten, die erforderlich sind, um das Ziel ohne Umwege zu erreichen. Es gibt somit 4 verschiedene Zustände:
Ecke A: Zustand 3 ( D.h.: Die Entfernung vom Ziel beträgt 3 Kanten )
Ecken B , D , E: Zustand 2
Ecken C , F , G: Zustand 1
Ziel: Zustand 0

Die Wahrscheinlichkeiten für die Übergänge zwischen den einzelnen Zuständen sind in der folgenden Tabelle festgehalten.

Die möglichen Übergänge lassen sich wie folgt veranschaulichen:

Für den Erwartungswert E(X) einer Zufallsgröße X gilt:     E(X) = ∑X_i*P(X_i)       (*)

Folgende Wege sind denkbar:
a) Zustand 3 --> Zustand 2 --> Zustand 3                                X₁*P(X₁) = [E(X) + 2]*(1/1)*(1/3)
b) Zustand 3 --> Zustand 2 --> Zustand 1 --> Zustand 2         X₂*P(X₂) = [E(X) + 2]*(1/1)*(2/3)*(2/3)
c) Zustand 3 --> Zustand 2 --> Zustand 1 --> Zustand 0         X₃*P(X₃) = [3]*(1/1)*(2/3)*(1/3)

Somit ergibt sich (*) zu :                     E(x) = [E(X) + 2]*(1/1)*(1/3) + [E(X) + 2]*(1/1)*(2/3)*(2/3) + [3]*(1/1)*(2/3)*(1/3)

                                                            E(X) = [E(X) + 2]/3 + 4*[E(X) + 2]/9 + 3*2/9          →          E(X) = 10

-----------------------------------------------------------------------------------------------------------------------------------------------------------

Bei MARKOW-Ketten ( Um ein solches Experiment handelt es sich hier ) ist auch eine Lösung mit Hilfe der Übergangsmatrix möglich:

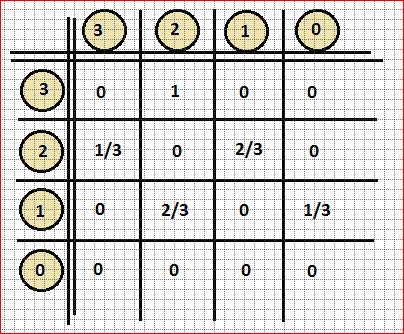
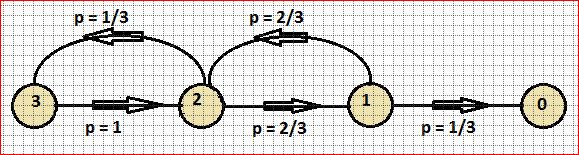
A=		A ( Übergangsmatrix ) enthält die Aufenthaltswahrscheinlichkeiten an den 8 Ecken des Quaders. Ecke 1 entspricht dabei der Ecke A in obiger Darstellung des Quaders. Zuordnungen: A(Start): 1 ; B: 2 ; C: 3 ; D: 4 ; E: 5 ; F: 6 ; G(Ziel): 7 ; H: 8 A[2][6] gibt somit die Wahrscheinlichkeit dafür an, dass sich der Käfer, so er sich jetzt im Punkt 2 ( also in B ) befindet, nach dem nächsten Kantengang im Punkt 6 ( also F ) befindet. An enthält die Aufenthaltswahrscheinlichkeiten nach den n-ten Zug. Von Interesse ist hier die Wahrscheinlichkeit, nach n Zügen von der Startposition 1 zum Ziel 7 zu gelangen. Diese Wahrscheinlichkeit findet sich in An[1][7]
A3=		A3[1][7] = 0.22222... besagt, dass der Käfer, ausgehend vom Start 1, das Ziel 7 nach der dritten Kante mit der Wahrscheinlichkeit 2/9 erreicht hat !
Aus der Quadergeometrie folgt unmittelbar, dass     An[1][7] = 0     für alle geradzahligen n gelten muss. Durch Potenzieren der Übergangsmatrix A ergeben sich folgende Wahrscheinlichkeiten: A3[1][7] = 2 / 32 A5[1][7] = (2 * 7) / 34 A7[1][7] = (2 * 72) / 36 A9[1][7] = (2 * 73) / 38 . . A2i - 1[1][7] = (2 * 7i-2) / 32i - 2 Aus     E(X) = ∑Xi*P(Xi)       folg somit: 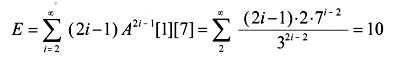Zurück