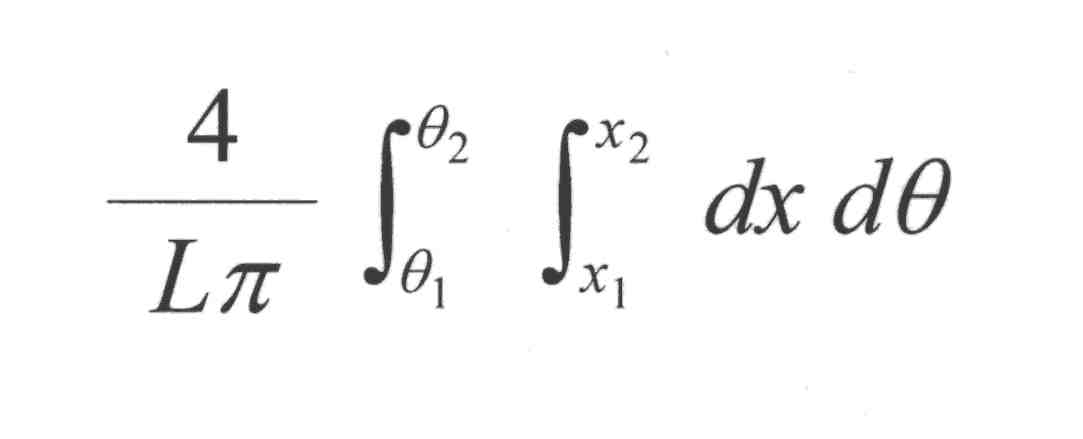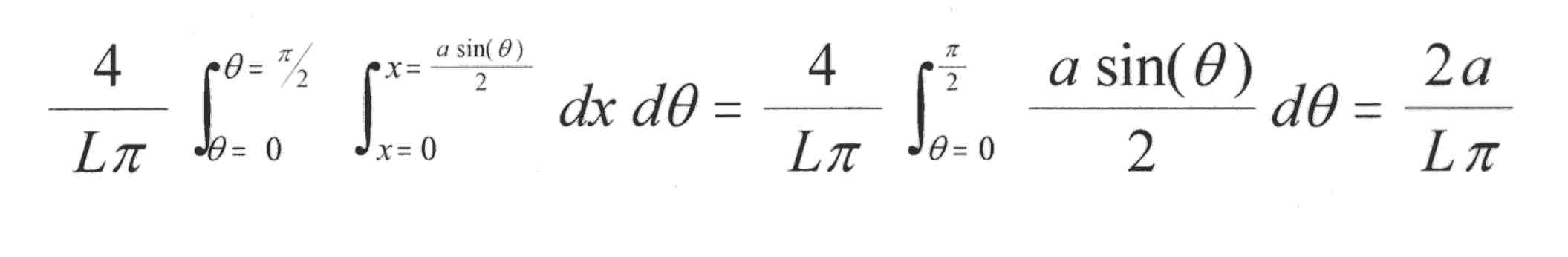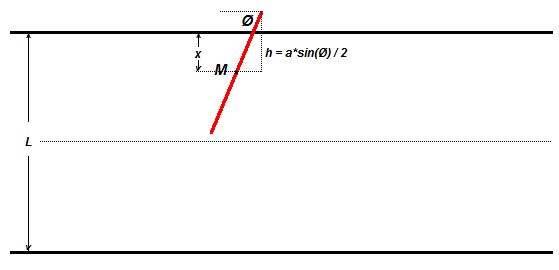
Lösungsskizze zum BUFFONsches Nadelproblem

Man lässt eine Nadel der Länge a über liniertem Papier ( Linienabstand L > a ) fallen. Mit welcher Wahrscheinlichkeit schneidet die Nadel eine Linie ?

Die Nadel schneidet immer dann eine Linie, wenn h >= x gilt !!

x: Abstand des Nadelmittelpunktes von einer Linie
Ø: Winkel zwischen Nadel und Linie

Für die Zufallsgrößen x und Ø gelten folgende Wahrscheinlichkeiten:

P(x ε dx) = dx/(L/2) = 2 dx/L      →      P(x1 ≤ x ≤ x2) = 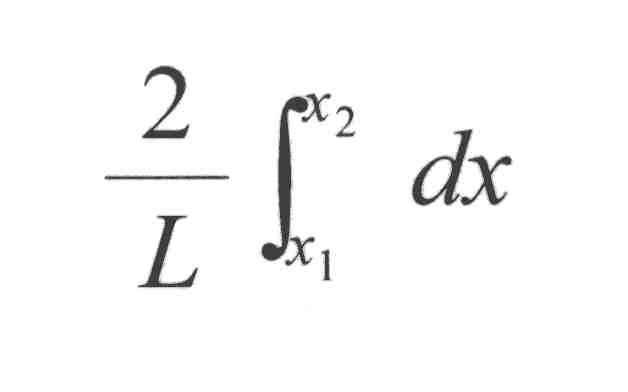( Wahrscheinlichkeit, dass der Nadelmittelpunkt M in einem Streifen x1 ≤ x ≤ x2 zu liegen kommt. )

P(Ø ε dØ) = dØ/(π/2) = 2 dØ/π      →      P(Ø1 ≤ Ø ≤ Ø2) = 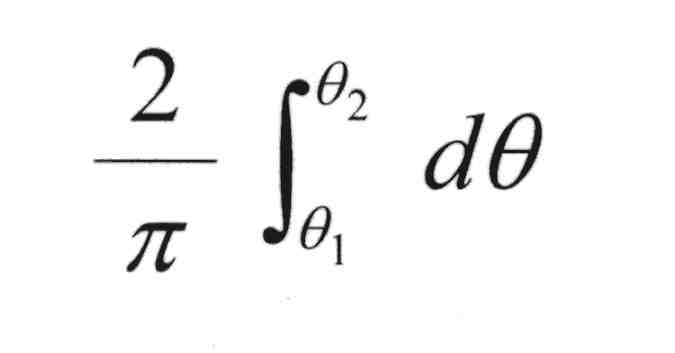( Wahrscheinlichkeit, dass Ø1 ≤ Ø ≤ Ø2 gilt.)
Die gemeinsame Wahrscheinlichkeit stellt das Produkt der Einzelwahrscheinlichkeiten dar:     P( Ø1 ≤ Ø ≤ Ø2   Λ   x1 ≤ x ≤ x2 ) =
Für   Ø ε [ 0 , π/2 ]   und   x ε [ 0 , a*sin(Ø)/2 ]   folgt somit:     P =


Bild 2 		Ein Näherungswert für die Wahrscheinlichkeit P lässt sich mit Hilfe von Computersimulationen ermitteln ( Siehe Bild 2 ). Damit liefert das Buffon-Problem einen interessanten Beitrag zum Thema "Approximation der Kreiszahl π" !.

Bild 2 ist das Ergebnis einer Simulation mit 1000 Nadeln der Länge 2[LE]. Der Abstand der horizontalen Linien wurde mit 3[LE] veranschlagt. Alle rot eingefärbten Nadeln ( insgesamt 424 ) schneiden oder berühren eine der beiden Linien.
Somit liefert die Simulation eine Buffon-Wahrscheinlichkeit    P = 424/1000 = 0,424. ( Das bedeutet eine Abweichung vom theoretischen Wert um 4/10000 ).
Benützt man das Ergebnis zur Approximation der Kreiszahl π , so ergibt sich eine Abweichung um weniger als 0,1% !

Zurück zur Aufgabenstellung