 |
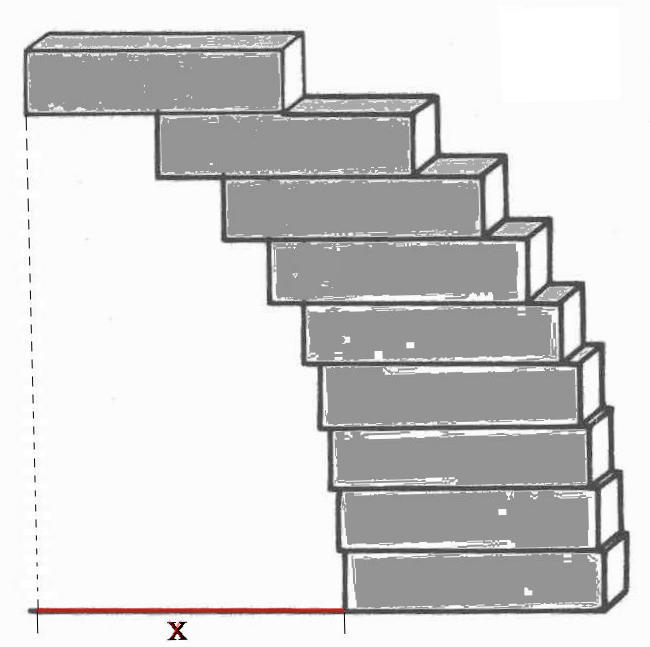
Angenommen, ein Steinmetz verfüge über eine unbegrenzte Menge kongruenter Quader ( gleiches Gewicht, gleiche Abmessungen, homogene Massenverteilung ). Werden diese, wie in der Skizze, so übereinander gelegt, dass der entstehende Bogen gerade nicht zusammenfällt, so wächst der Abstand X des obersten zum untersten Quader zunächst von Stein zu Stein.
Wie groß kann X im Idealfall werden, wenn die Quader die Länge l besitzen?
|