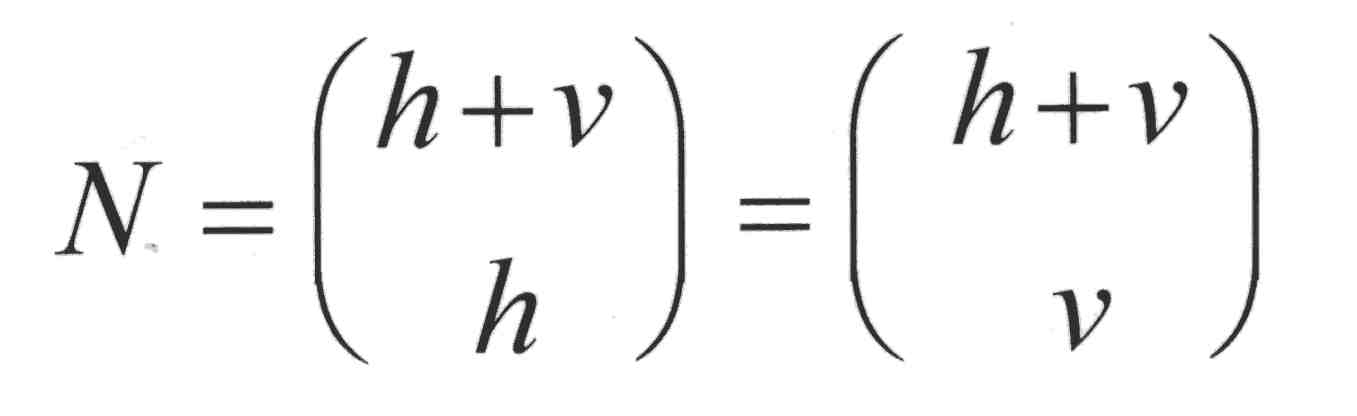Viele Aufgaben aus der Kombinatorik ( Warteschlangen , Ruinproblem, Irrfahrten ... ) lassen sich auf das anschauliche Problem der
Minimalwege in einem Quadratgitter zurückführen.
h: Anzahl der "Schritte" in horizontaler Richtung
v: Anzahl der "Schritte" in vertikaler Richtung
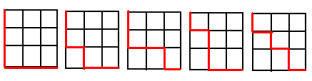 |
In nebenstehender Skizze sind einige Minimalwege in ein 3x3-Gitter eingezeichnet. Um vom Startpunkt links-oben ohne Umwege zum Ziel rechts-unten zu gelangen, muss man
insgesamt 3 + 3 = 6 "Schritte" tun. Völlig unabhängig von der Wegewahl, geht man stets 3 Schritte in horizontaler (h = 3) und drei Schritte in vertikaler Richtung (v = 3). Die Formel zur Berechnung der Pemutationen mit Wiederholungen gibt Auskunft
über die Anzahl der möglichen Anordnungen:
P( 6 ; 3 , 3 ) = 6! / ( 3! * 3! ) = 20 In einem 3 x 3-Gitter gibt es somit 20 verschiedene Minimalwege.
|
Für ein h x v-Gitter lässt sich o.a. Formel wie folgt modifizieren: P( h + v; h , v ) = ( h + v )! / ( h! * v! ) := N (*)
Unter Zuhilfenahme der Formel zur Berechnung von Kombinationen ( ohne Wiederholungen ) lässt sich (*) wie folgt schreiben: 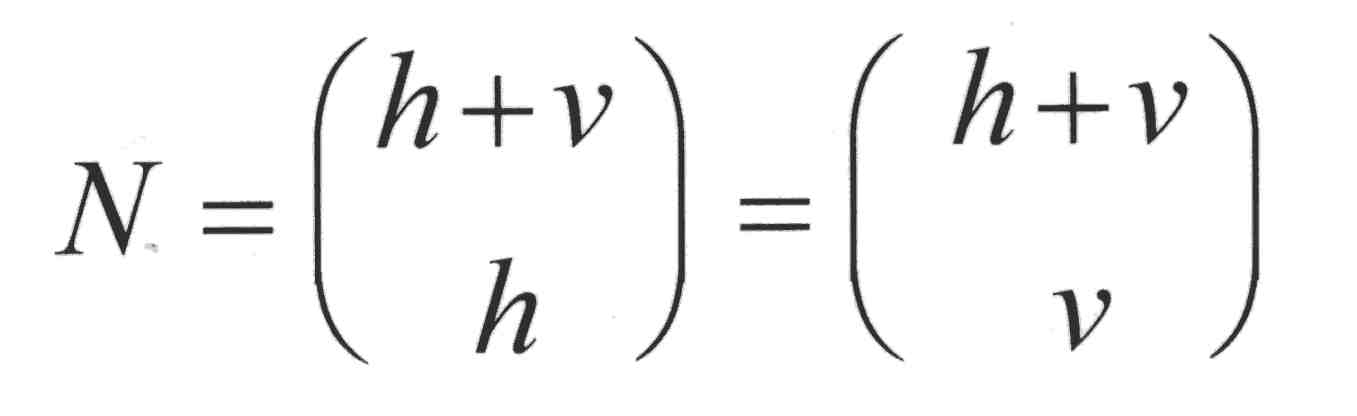
Im konkreten Fall der Aufgabenstellung legt John 16 - 7 = 9 Straßenabschnitte in Ost-West-Richtung und 24 - 12 = 12 Abschnitte in Nord-Süd-Richtung zurück. Daraus ergeben sich mit o.a. Formel 293930 verschiedene Wege vom Arbeitsplatz
zur Privatwohnung!
Analoge Überlegungen zeigen, dass für den Weg vom Arbeitsplatz zur Kneipe 24310 Varianten denkbar sind. Für die Wahrscheinlichkeit W, dass John zufällig an seiner Kneipe vorbei fährt, ergibt sich somit der Quotientenwert
W = 24310/293930 = 0,0827
|
|