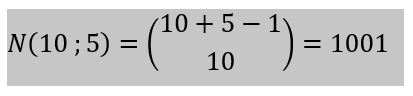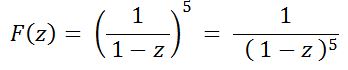Lösungsskizze zum Osterhasen-Problem
Problemstellung:
Mit F Farben sollen E Eier eingefärbt werden. Wie viele verschiedene Möglichkeiten sind denkbar?
Lösung mittlels Formel:
Die Aufgabenstellung impliziert die Berechnung von Kombinationen mit Wiederholungen!
In der Formelsammlung findet sich dazu folgende Formel:

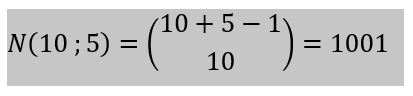
Lösung mittlels der ERZEUGENDEN FUNKTION:
Eleganter - und universeller anwendbar - ist ein Lösungsansatz unter Verwendung der Erzeugenden Funktion!
In jede unserer 'Schubladen' passen beliebig viele Eier. Damit lautet unsere EZF im vorliegenden Fall: EZF:
( 1 + z + z2 + z3 + z4 + ...)5 = 1/( 1 - z )5
Konkret: 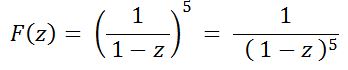
Taylor-Entwicklung: F(z) = 1z0 + 5z1 + 15z2 + 35z3 + 70z4 + 126z5 + 210z6 + 330z7 + 495z8 + 715z9 + 1001z10 +
1365z11 + 1820z12 + 2380z13 + ...
10 Eier können somit auf 1001 verschiedene Arten mit 5 Farben gefärbt werden.
__________________________________________________________________________________________________________________________________________________________
Die Universalität der ERZEUGENDEN FUNKTION wird u.a. durch ihre Einsetzbarkeit bei folgender - etwas modifizierter - Aufgabenstellung erkennbar:
Wie viele Möglichkeiten N gibt es, mit 5 unterschiedlichen Farben E Eier zu färben, wenn folgende Restriktionen zu berücksichtigen sind:
a: Die rote Farbe reicht maximal für 4 Eier!
⇒ EZF(a): (1 + z + z2 + z3 + z4 )
b: Die Anzahl der geben Eier soll zwischen 2 - 5 liegen. ⇒
EZF(b): (z2 + z3 + z4 + z5)
c: Ein grünes Ei soll mindestens dabei sein!
⇒ EZF(c): (z + z2 + z3 + z4 + z5)
d: Die beiden restlichen Farben unterliegen keinerlei Restriktionen! ⇒
EZF(d): 1/( 1 - z )2
Das Produkt aus den einzelnen EZF's stellt die aufgabenrelevante , endgültige, EZF dar!!
EZF: (1 + z + z2 + z3 + z4 ) *
(z2 + z3 + z4 + z5)
* (z + z2 + z3 + z4 + z5) * 1/( 1 - z )2
TAYLOR-Entwicklung: 1*z3 + 5*z4 + 15*z5 + 35*z6 + 69*z7 + 119*z8
+ 185*z9 + 265*z10 + 355*z11 + 451*z12 + ....