Lösungsskizze zum Gras-sharing

Aufgabenstellung

Ein Schrebergärtner hält sich eine Kuh und eine Ziege als Haustiere. Die üppige Wiese im Schrebergarten bietet ausreichend Futter. Zum Schutz des nahegelegenen Gemüsegartens werden beide Tiere während der Futtersuche angepflockt. Die Kuh an einer 6 Meter langen Leine, die Ziege hat lediglich einen Aktionsradius von 4 Meter zur Verfügung. Da die beiden Pflöcke nur eine Entfernung von 7 Meter besitzen, wird ein Teil der zur Verfügung stehenden Fläche von beiden Tieren genutzt.
Um wie viele Quadratmeter ist die Weidefläche, die der Kuh alleine zur Verfügung steht, größer als die Fläche, die alleine der Ziege vorbehalten ist?

L ö s u n g s s k i z z e

Analytische Darstellung eines Kreises   K   mit Radius r und dem Miittelpunkt M(a,b):

K:    (x - a) 2 + (y - b) 2 = r 2

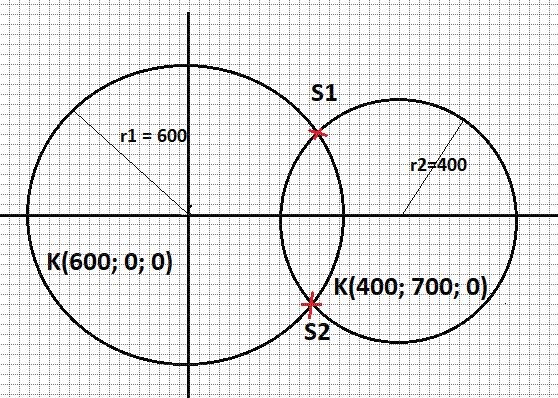
Schnittpunktskoordinaten S1 und S2 ermitteln

K1:   x 2 + y 2 = 62       -->      y2 = 36 - x2                         K2:   (x - 7)2 + y 2 = 42    

EINSETZEN:       (x - 7)2 + (36 - x2) = 16     -->     14x = 69

    -->    x = 4,93

Y-KOORDINATE berechnen:            -->       4,932 + y2 = 36            -->      y = 3,42

S1(4,93 ; 3,42)         //         S2(4,93 ; - 3,42 )

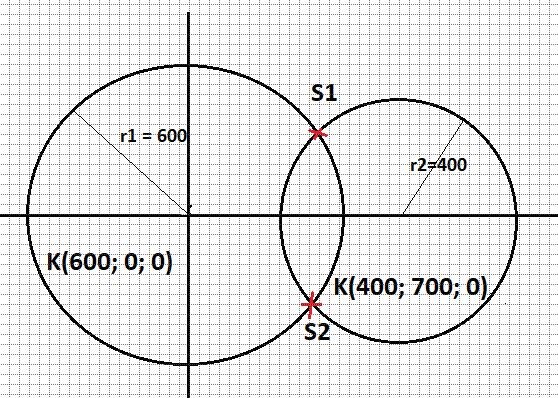
Fläche des roten Segments

Winkel α = Winkel (S2; M1; S1)   berechnen:
tan(α/2) = TS1 / TM1     ⇒     α = 2*atan(3,42/4,83)     ⇒    α = 69,5 º

Sektorfläche ASek von Sektor S2;M1;S1 berechnen:
ASek = r2 * π * α / 360 = 36 * π * 69,5 / 360 = 21,834

Fläche des Dreiecks S2;M1;S1 berechnen:
ADreieck = S1S2 * TM1 / 2 = 16,86
ASegment = ASek - ADreieck = 21,834 - 16,86 = 4,974 = Arot

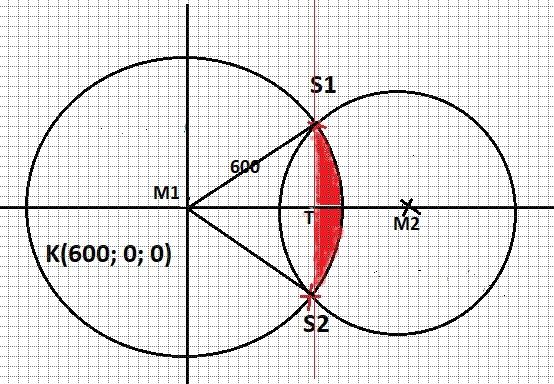
Fläche des gelben Segments

Die Fläche des gelben Segments berechnet sich analog zur Berechnung der roten Fläche!
ERGEBNIS:     Agelb = 9,3448

Fläche der Farblinse und Lösung

Die gemeinsam genutze Grasfläche Agemeinsam = Agelb + Arot = 9,3448 + 4,974 = 14,319m2

Die Kuh 'bearbeitet' somit ein Areal von 62 * π - 14,319 = 98,778m2 alleine.

Der Ziege stehen 42 * π - 14,319 = 35,945m2 zum alleinigen Gebrauch zur Verfügung!

ADelta = 98,778 - 35,496 = 62,83m2 !


Zur Aufgabenstellung