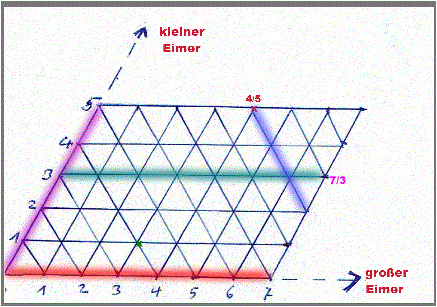
Die Aufgabe lässt sich mit Hilfe eines geeigneten Koordinatengitters gut veranschaulichen und leicht lösen!
Rote Linie: (0/0) --> (7/0) Der große Eimer wird mit Flusswasser aufgefüllt!
(7/0) --> (0/0) Der große Eimer wird entleert!
Lila Linie: (0/0) --> (0/5) Der kleine Eimer wird mit Flusswasser aufgefüllt!
(0/5) --> (0/0) Der kleine Eimer wird entleert!
Blaue Linie: (4/5) --> (7/2) 3 Liter des kleinen Eimers werden in den großen Eimer umgeleert!
(7/2) --> (4/5) 3 Liter des großen Eimers werden in den kleinen Eimer geschüttet!
Grüne Linie: (0/3) --> (7/3) Dergroße Eimer wird mit 7 Liter Flusswasser gefüllt!
(7/3) --> (0/3) Der große Eimer wird zur Gänze entleert!
Da die Gefäße über keine Kalibrierung verfügen, müssen die Koordinaten aller Ausgangs- und Endpunkte
ausnahmslos auf den Begrenzungslinien des Parallelogramms liegen!!
Graphische Lösung des Umschüttproblems
1. Schritt: (0/0) --> (7/0) ( Der große Eimer wird mit Flusswasser gefüllt )
2. Schritt: (7/0) --> (2/5) ( Der kleine Eimer wird mit 5 Liter aus dem großen Eimer gefüllt )
3. Schritt: (2/5) --> (2/0) ( Der kleine Eimer wird entleert )
4. Schritt: (2/0) --> (0/2) ( Der Inhalt des großen Eimers wird in den kleinen Eimer gegossen )
5. Schritt: (0/2) --> (7/2) ( Der große Eimer wird mit 7 Liter Flusswasser gefüllt )
6. Schritt: (7/2) --> (4/5) ( Der kleine Eimer wird mit 3 Liter aus dem großen Eimer aufgefüllt )
7. Schritt: (4/5) --> (4/0) ( Der kleine Eimer wird entleert )
8. Schritt: (4/0) --> (0/4) ( Der Der Inhalt des großen Eimers wird in den kleinen Eimer gekippt )
9. Schritt: (0/4) --> (7/4) ( Der große Eimer wird mit Flusswasser gefüllt )
10. Schritt: (7/4) --> (6/5) ( Der kleine Eimer wird mit einem Liter aus dem großen Eimer aufgefüllt )
Nach insgesamt 10 Arbeitsschritten enthält der große Eimer somit exakt die geforderten 6 Liter!