1) Wie viel Partitionen ( unterschiedliche Möglichkeiten ) gibt es, eine n-elementige Menge in k nichtleere, paarweise disjunkte Teilmengen zu zerlegen ?
2) Auf wie viel Arten lassen sich n Gegenstände ( hier: Geschenke ) an k Personen aushändigen ?
Zu 1)
Beispiel: M = { A,B,C,D } ist eine n = 4-elementige Menge. Wie viele Möglichkeiten ( Partitionen ) gibt es, die Menge in 3 nichtleere, paarweise disjunkte Teilmengen aufzuteilen ?
Man findet leicht, dass es insgesamt 6 Möglichkeiten gibt:
a) {A,B} ; {C} ; {D}
b) {A,C} ; {B} ; {D}
c) {A,D} ; {B} ; {C}
d) {A} ; {B,C} ; {D}
e) {A} ; {B,D} ; {C}
f) {A} ; {B} ; {C,D}
Bei der vorliegenden Aufgabe gilt es, insgesamt 7 Elemente ( Geschenke ) in 4 Teilmengen ( 4 Enkel ! ) zu zerlegen. Die Vielzahl der Möglichkeiten verbietet in diesem konkreten Fall eine Vorgehensweise wie in o.a. Beispiel. Eine allgemeine Lösung des Problems gelang erstmals dem schottischen Mathematiker James STIRLING ( 1692 - 1770 ) mit Hilfe der nach ihm benannten Formel:
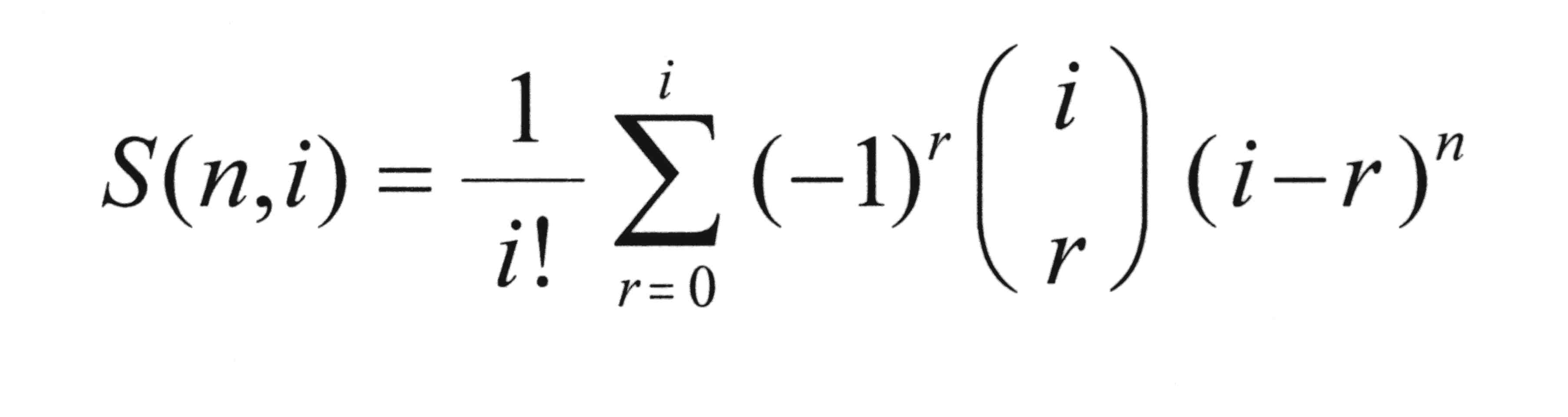
Im konkreten Fall des vorliegenden Problems ist n = 7 ( Geschenke ) und i = 4 ( Kinder ). Mit Hilfe o.a. Formel ergibt sich: S(7,4) = 350 .
Zu 2)
k Teilmengen lassen sich an k Kinder ( hier: 4 Kinder ) auf k! unterschiedliche Arten verteilen.
Somit ergeben sich Ngesamt = S(7,4) * 4! = 350 * 24 = 8400 Möglichkeiten, die 7 Geschenke auf 4 Kinder zu verteilen.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Eleganter lässt sich die Aufgabe mit Hilfe einer geeigneten Erzeugenden Funktion lösen. Zur Vorbereitung wird auf die Lösungsskizzen zu den beiden Osterhasen-Problemen verwiesen!
Den Part der Schubladen ( bzw. Farben ) spielen diesmal die Enkelkinder. Jedes der insgesamt K Kinder kann mit mindestens einem Geschenk rechnen. Würden die Geschenke auf Schubladen verteilt, so müsste die EF lauten:
EF(z) = ( z1 + z2 + z3 + + z4 + ..., )K Da die Kinder - im Gegensatz zu den Schubladen - untereinander unterscheidbar sind, und i Geschenke auf i Kinder jeweils auf i! Arten verteilt werden können, lautet die Erzeugende Funktion im vorliegenden Fall:
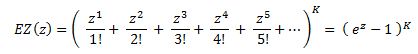
Setzt man für die Anzahl K der Kinder ( im vorliegenden Problem ist K = 4 ) die entsprechende Zahl ein, so lautet die Erzeugende Funktion: EF(z) = ( ez - 1 )4
Die Taylorentwicklung führt zu:
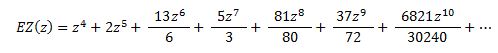
Dieses Ergebnis muss nun so umgeformt weren, dass es der ursprünglichen Potenzreihendarstellung entspricht ( im Nenner steht die jeweilige Fakultät! ). Das führt zur Potenzreihe:
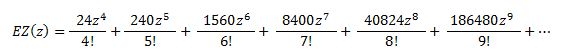
Dieser Reihe entnimmt man unmittelbar, dass es insgesamt 8400 Möglichkeiten gibt, 7 Geschenke auf 4 Kinder zu verteilen. ( Bei 9 Geschenken hat Opa schon 186480 unterschiedliche Möglichkeiten! )