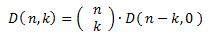Lösungsskizze zur Freigang-Aufgabe
Derangement-Zahlen

Fragestellung: Nach einem Freigang torkeln n volltrunkene Matrosen in die nächstbeste Kajüte Wie groß ist die Wahrscheinlichkeit, dass höchstens k von ihnen im eigenen Bett schlafen?

Zunächst wird man versuchen, eine Antwort auf folgende Frage zu finden: Wie viele Möglichkeiten gibt es, n Personen ( Gegenstände ) so auf m Positionen so zu verteilen, dass keine Person auf seinem angestammten Platz steht? Mathematisch gesehen geht es um die Frage nach der Anzahl der fixpunktfreien Permutationen einer n-elementigen Menge. Am Beispiel einer m = 4-elementigen Menge lässt sich das Problem noch bequem durch Abzählen lösen. Vier Elemente lassen sich auf 4! Arten permutieren: ( 1 2 3 4 ) ( 1 2 4 3 ) ( 1 4 2 3 ) ( 1 3 2 4 ) ( 1 3 4 2 ) ( 1 4 3 2 ) ( 2 1 3 4 ) ( 2 1 4 3 ) ( 2 4 1 3 ) ( 2 3 1 4 ) ( 2 3 4 1 ) ( 2 4 3 1 ) ( 3 2 1 4 ) ( 3 2 4 1 ) ( 3 4 2 1 ) ( 3 1 2 4 ) ( 3 1 4 2 ) ( 3 4 1 2 ) ( 4 2 3 1 ) ( 4 2 1 3 ) ( 4 1 2 3 ) ( 4 3 2 1 ) ( 4 3 1 2 ) ( 4 1 3 21 ) Die fixpunktfreien Permutationen sind rot gekennzeichnet, es gibt deren 9. Somit gilt:   D(4,0) = 9.   D steht hierbei für DERANGEMENT-Zahl. D(n,k) steht für die Anzahl der Permutationen ( in einer n-elementigen Menge ) mit genau k Fixpunkten.

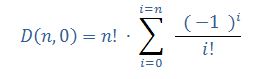Die Anwendungsbreite der Abzählmethode beschränkt sich natürlich auf kleine n. Bei zunehmender Mächtigkeit greift man auf eine der folgenden Formeln ( Herleitung weiter unten! ) zur Bestimmung der Derangement-Zahlen zurück:    ;    D(n,0) = ROUND( n!/ e )    ;     D( n,0 ) = n*D( n-1,0 ) + (-1)n      mit   D(0,0 ) = D( 1,0 ) = 0 Derangements mit genau k Fixpunkten :

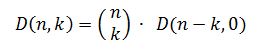
In der Aufgabenstellung ist n = 12 und k <= 3. D( 12,0 ) = 176214841   ;    D( 12,1 ) = 176214840    ;     D( 12,2 ) = 88107426    ;    D( 12,3 ) = 29369120 Somit ergibt sich für die gesuchte Wahrscheinlichkeit:   P = [ D( 12,0 ) + D( 12,1 ) + D(12,2 ) + D( 12,3 ) ] / ( 12! ) = 0,981

Hereitung der Formel: Sei A die Menge aller Permutationen von M = { 1, 2, 3, ... , n }. Ai bezeichne die Menge aller Permutationen, die das i-te Element zum Fixpunkt hat. Dann ist   D( n,0) = | A \ ( A1 ∪ A2 ∪ A3 ∪ ... ∪ An ) | = | A | - | A1 ∪ A2 ∪ A3 ∪ ... ∪ An | Im Folgenden wird zunächst die Anzahl F der Permutationen berechnet, die mindestens +über einen Fixpunkt verfügen.   F = | A1 ∪ A2 ∪ A3 ∪ ... ∪ An | Mit der Formel von Sylvester:   F = ∑ Ai - ∑( Ai ∩ Aj = + ∑ ( Ai ∩ Aj ∩ Ak ) - ...... + ( -1 )n-1 ( Ai ∩ Aj ∩ ... ∩ An ) Die einzelnen Summen lassen sich wie folgt berechnen: -   Wird das i-te Element der Menge fixiert, so können die restlichen Elemente noch auf  ( n - 1 )!   Arten permutieren. 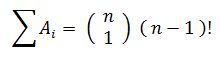Da die Menge über n Elemente verfügt   →     -   Wird sowohl das i-te, als auch das k-te Element der Menge fixiert, so können die restlichen Elemente noch auf  ( n - 2 )!   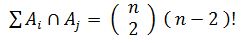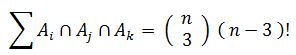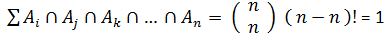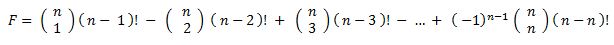Arten permutieren    →     -   In Analogie zu den bisherigen Überlegungen folgt:    -    Die Anzahl F der Permutationen mit mindestens einem Fixpunkt berechnet sich somit zu:    Die Wahrscheinlichkeit P(F), dass eine Permutation über mindestens einen Fixpunkt verfügt ist somit: 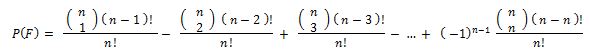     → P(F) = 1 / 1! - 1 / 2! + 1 / 3! - --- + ( -1 )n - 1 * 1 / n! Für das Komplementärereignis  ( Eine Permutation besitzt keinen Fixpunkt ) gilt somit:    P( D( n,0 ) ) = 1 - P(F) = 1 - 1/1! + 1/2! - 1/3! + ... ... (-1)n * 1/n!    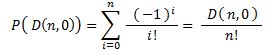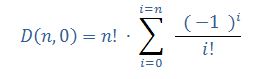→        →     Für    n   →   ∞  ist die Summe auf der rechten Gleichungsseite identisch mit der Taylorentwicklung von  e-1. Die Konvergenz erfolgt so rasch, dass    D( n,0 ) = ROUND( n! / e )   das exakte Ergebnis für alle   n   ∈   N    liefert! Für die Anzahl der Permutationen mit genau k Fixpunkten folgt daraus unmittelbar:   Zurück zur Aufgabenstellung