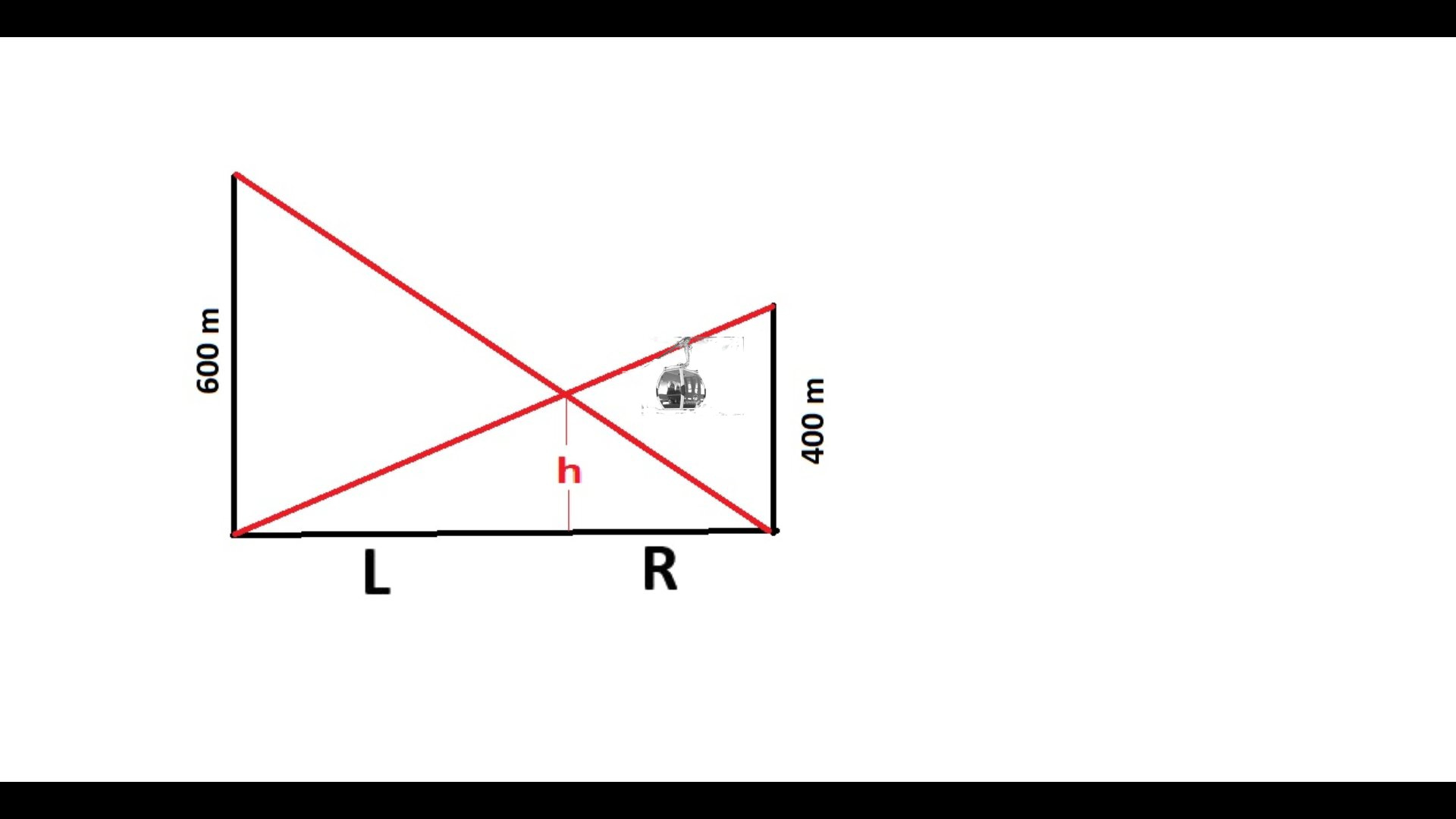
Die straff gespannten Zugseile zweier gegenläufiger Gondeln ( in der Skizze rot gefärbt! ) kreuzen sich in der Höhe h über dem Talboden.
Die Höhe h soll berechnet werden!
|
L Ö S U N G
Zur Bestimmung von h bietet sich der Strahlensatz an!
Für das linke Dreieck ( Höhe = 600 Meter ) gilt: ( L + R ) / 600 = R / h
Für das rechte Dreieck ( Höhe = 400 Meter ) gilt: ( L + R ) / 400 = L / h
Addition beider Gleichungen:
(L + R)/600 + (L + R)/400 = R/h + L/h
Eine Gleichung mit drei Unbekannten - Das funktioniert nicht!!
( Jedenfalls im Allgemeinen )
Durch Ausklammern erhält man: (L + R)[ 1/600 + 1/400 ] = [ L + R ] ( 1/h )
Division durch den gemeinsamen Faktor [ L + R ]: ( 1/600 + 1/400 ) = 1/h
Die letzte Gleichung zeigt, dass L und R keinerlei Einfluss auf die Höhe des Kreuzungspunktes der Seile haben!! Sie
beinhaltet nur noch eine Variable und sollte somit eindeutig lösbar sein!
h = 240[m]
|